畳み込みについての基本的イメージは前の記事で説明しました。本記事では、畳み込み演算(Convolution Operation)がコンピュータ上でどの様に行われているかについて見ていきます。
受容野をスライドさせる
前の記事で紹介した入力画像上をスライドする青い四角は、神経細胞の樹状突起のある領域に習ってニューロンの受容野(Receptive Field)と呼ばれています。受容野のそれぞれの入力値\(x_{ij}\)に対して、ニューロンjは重み\(w_{ij}\)を持ちます。前の記事での3✕3の例では、下図の入力\(x\)は\({x_{00},x_{01},x_{02},x_{10},x_{11},x_{12},x_{20},x_{21},x_{22}}\)の9個の値、同様に重み\(w\)は\({w_{00},w_{01},w_{02},w_{10},w_{11},w_{12},w_{20},w_{21},w_{22}}\)の9個になります。
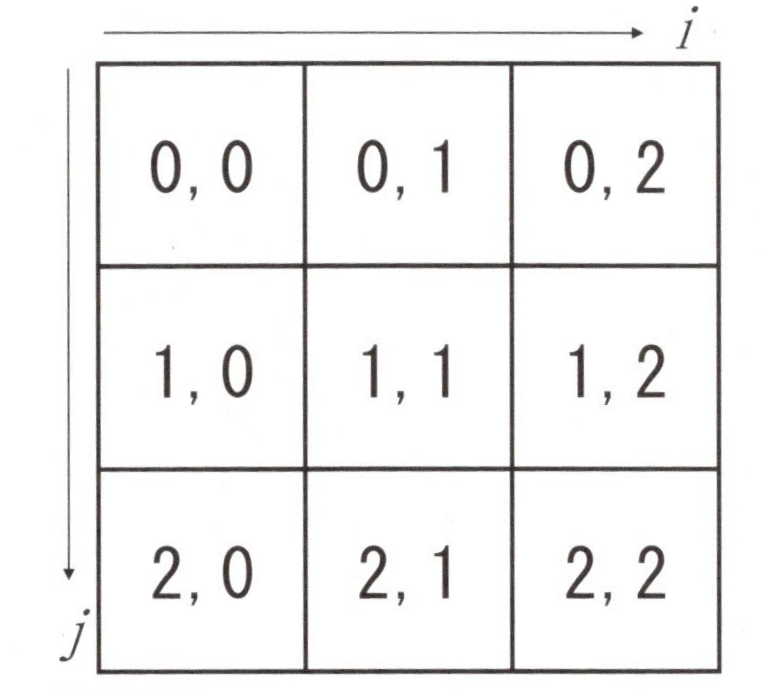
3✕3に対応する入力\(x\)と重み\(w\)
ここで、\(i\)と\(j\)は入力値とそれに対応する重みの何番目かを表します。ある入力画像の領域に着目した時、次のような式で表されます。
\(
\begin{eqnarray}
y=wsm(w,x)=\displaystyle \sum_{i,j} w_{ij}・x_{ij} \tag{1}
\end{eqnarray}
\)
\(wsm\)は重み付き総和モデルを表します。具体的には、ニューロンが1つの部分領域にフォーカスされているとき、この部分領域の\(x_{ij}\)の値は、それぞれが重み\(w_{ij}\)に掛け合わされ、夜の合計値が出力\(y\)として生成されます。
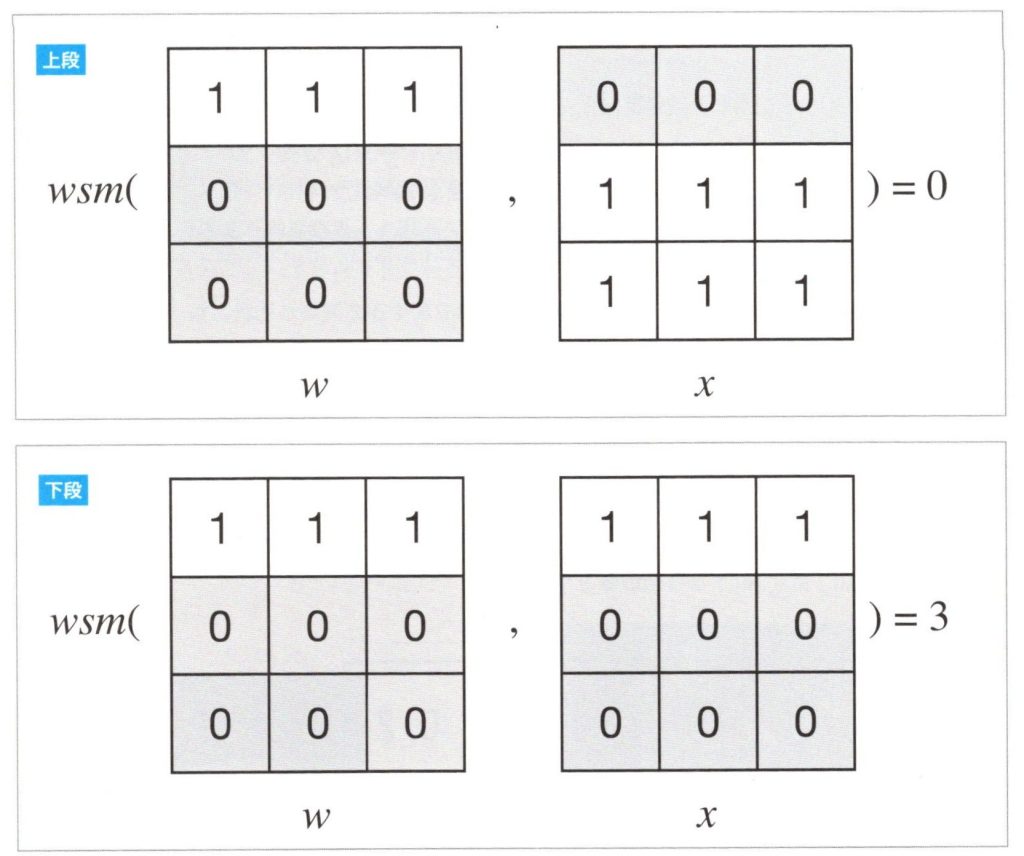
畳み込みニューロンの大きい出力と小さい出力の例
一般的にニューラルネットワークでは、入力値と重みの値の両方の幅(range)を[0,1]の小さな幅になるようにコントロールします。この入力値\(x\)で\(wsm\)の式を計算すると、入力\(x\)と重み\(w_{ij}\)が大きく違っていたら非常に小さな出力値\(y\)になります。このような場合、このニューロンは発火できません。入力\(x\)と重み\(w_{ij}\)が似ているときにのみ、大きな出力値\(y\)を得ることが出来るのです。上図はこの畳込み演算を利用した場合の、小さい値を出力する例(上段)と大きい値を出力する例(下段)です。
フォーカスの移動
このニューロンは、別の部分領域にスライドしながら同じ演算を繰り返します。このとき、次の領域に移動すると新しい入力値になります。この処理の流れは下図で表せます。
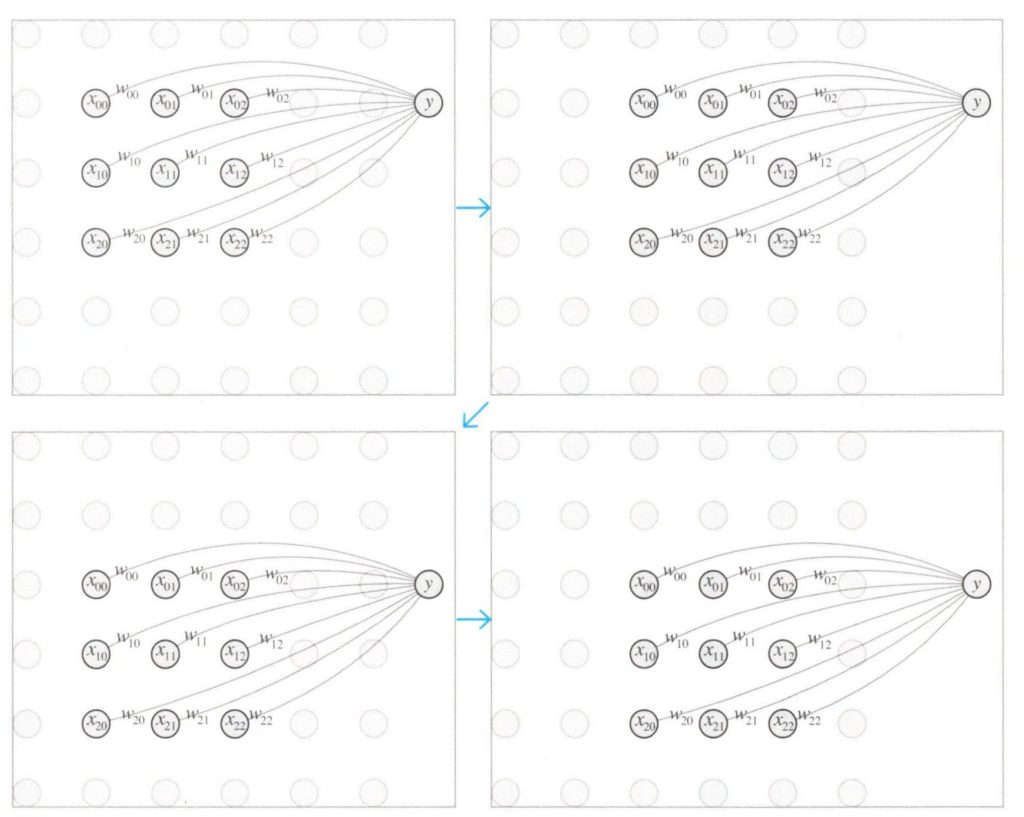
フォーカスの移動
1個のニューロンの受容野をスライドさせて入力値\(x\)を受け付けると、それぞれの部分領域に対して出力値\(y\)が得られます。この出力値\(y\)をまとめてセットにして下図(a)のようにすることで入力画像と同じ様な形を表す出力データを作ることが出来ます。6✕6の四角い入力データとすると、ニューロンの受容野は3✕3となり、出力データは4✕4の四角となります。下図(b)は、手書きの数字の画像に対して畳み込み処理をしたときの、画像全体に対するニューロンの受容野の対応関係の例です。
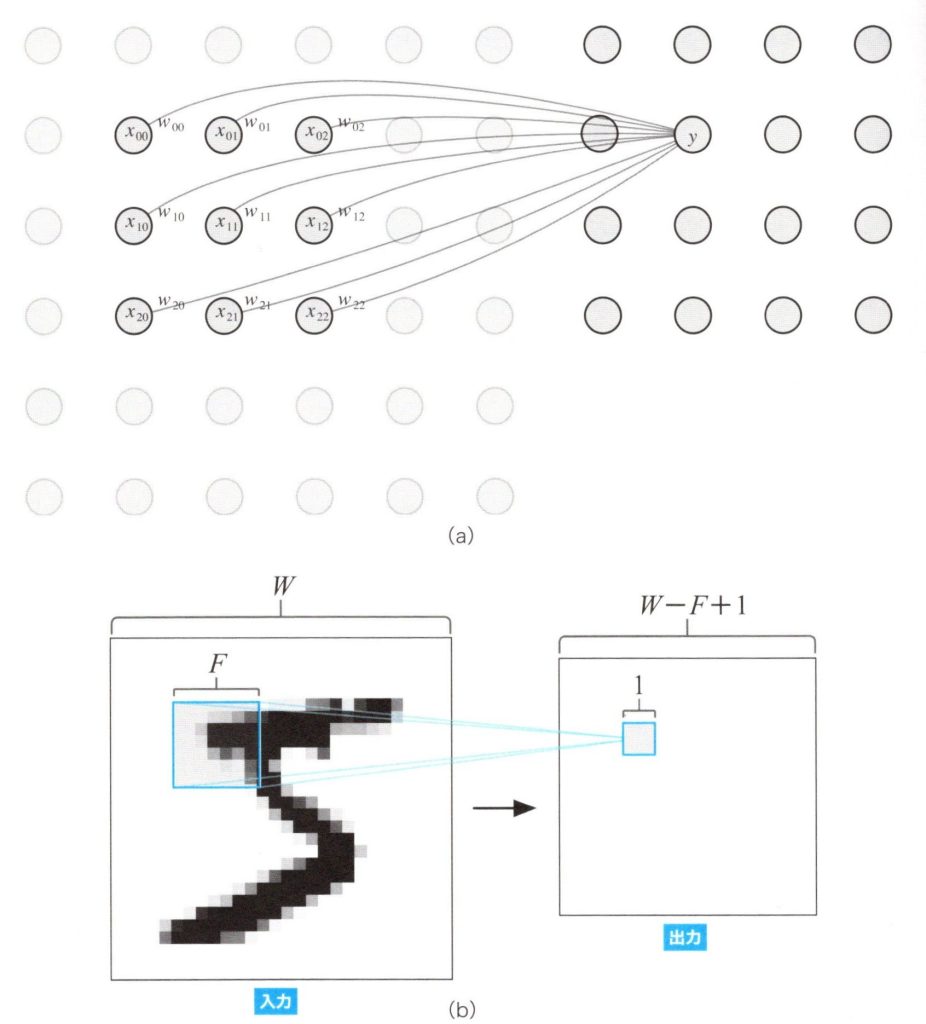
畳み込みニューロンの出力
これは畳み込みニューロンの形を計算するのにとても便利な方法です。入力データの幅と長さを\(W\)としたとしたとき、ニューロンの受容野の幅と長さを\(F\)とすると、出力の幅と長さは\(W-F+1\)で表すことが出来ます。大雑把にいうと、畳み込みニューロンの出力データは、入力データの幅と長さから受容野の幅と長さを除いたサイズになるというわけです。