DX(データ分析・機械学習)関係に戻る
目次(ページ内リンク)
第1章 なぜ統計学が最強の学問なのか?
21世紀の現代において、統計学は「リテラシー」となっている。では、なぜ統計学の重要性が近年急上昇したのだろうか。その答えを一言でいえば、どんな分野の議論においても、データを集めて分析することで最速で最善の答えを出すことができるためである。
例えば、選択を誤れば10万人の命が失われるといった状況に置かれた状況を想定してみよう。その状況では何を根拠に判断を下すだろうか?そのようなときにあなたは上司の直感や経験だけに任せて決断を行うだろうか?また、10万人の命がかかった選択を、 何の根拠もなく権力者たちの意見だけで決定したとすれば、あなたはどう思うだろうか?
こうした大量の人命がかかった間違いの許されない選択において最善の答えを出すために、人類は19世紀のロンドンで、史上で初めて統計学の力を使って万単位の人命を奪う原因に戦いを挑んだ。原因不明な疫病を防止するための学問を「疫学」と呼ぶが、世界で最初の疫学研究は19世紀のロンドンで、コレラという疫病に対して行われた。この疫学の中でも統計学は大きな役割を果たす。当時のロンドンには高い教育を受けた科学者も医者も、優秀な役人も十分にいた。彼らの多くは聡明で論理的でもあっただろうが、残念なことにコレラの流行に対しては無力であった。要するに、知性も見識も十分にある彼らが知恵を絞って出したアイディアも、時間と労力をつぎ込んだ事業も、無駄か、もしくはむしろ有害であったのである。
では、彼らはいったいどうすべきだったのだろうか。それは下記で示すとおりである。
・コレラで亡くなった人の家を訪れ、話を聞いたり付近の環境をよく観察する。
・同じような状況下でコレラにかかった人と掛かっていない人の違いを比べる。
・仮説が得られたら大規模にデータを集め、コレラの発症/非発症と関連していると
考えられる「違い」について。どの程度確からしいか検証する。
頭やセンスや行動力に優れた人たちを集めて話し合わせただけでは、強力な解決策は出てこないし、むしろ握りつぶされることも多い。代わりに出てくるやり方が、一見理屈としては正しくても、無益もしくは有害であることもしばしばあるのである。
「疫学」という、データ統計解析に基づき最善の判断を下そう、という考え方は現在では医学の領域において欠くことのできないものとなった。
現代の医療で最も重要な考え方としてEBM(Evidence-Based Medicine)、日本語で言う「科学的根拠に基づく医療」というものがある。この科学的根拠のうち、最も重視されるものの一つが、妥当な方法によって得られた統計データとその分析結果、というわけである。
人間の体には不確実性が多く、データを取って分析すると、生理学的な理屈のうえでは正しいはずの治療法が効果を示さないケースや、経験と権威にあふれる大御所の医師たちがこれまで続けていた治療法がじつはまったくの誤りだった、という事例が少しずつ明らかになってくる。そのため、医師の経験と勘だけでなく、きちんとしたデータとその解析結果、すなわちエビデンスに基づくことで最も適切な判断をすべきだ、というのが現在医学において主流の考え方なのである。原因不明なのであれば、その原因を明らかにするために行なうべきことは、慎重かつ大規模なデータの収集であり、その適切な統計解析以外にはあり得ないのである。
エビデンスは議論をぶっ飛ばして最善の答えを提示する。エビデンスに反論しようとすれば理屈や経験などではなく、統計学的にデータや手法の限界を指摘するか、もしくは自説を裏付けるような新たなエビデンスを作るかといったやり方でなければ対抗できないのだ。
では、なぜ今、これほど統計学がさまざまな分野で重要視されるようになったのだろうか。データ間の関連性から因果関係を推論するという現代統計学の基本的な考え方は今世紀の前半にはほぼ確立していたし、主要な統計解析手法は1960年代頃にはほぼ出揃っていた。これだけ統計学がパワフルなものであるのならば、もっと前から社会の至るところで使われているべきじゃないか?という疑問ももっともだ。その答えは統計学自体ではなく、統計学を活用するための環境の変化にある。それは、大規模データを効率的に処理するための新しい製品の仕組みと性能が整ったのが現在であるため、という単純な答えである。
第2章 サンプリングが情報コストを激減させる
ビッグデータというバズワードが流行りはじめてずいぶん経つ。「ビッグデータ」というコンセプトにビジネスチャンスを期待する人間は、ハードウェアベンダーやシステムインテグレータ、コンサルティングファームなどさまざまな業界に存在している。ITにも統計学にも詳しいわけでもないないビジネス畑の評論家たちも、判を押したように「これからはビッグデータの時代だ」と言っている。
しかしながら、彼らは果たしてデータがビッグであること、あるいはデータをビッグなまま解析することが、どれだけの価値を生むのかどうか、果たして投資するコストに見合うだけのベネフィットが得られるのかどうか、わかっているのだろうか。データ処理が高速化することで、ウェブサービスはユーザー数が増えても快適なサービスを提供できるし、社内システムにおいてはより短時間で定例の集計作業を終えることにも繋がるかもしれない。それに伴って人件費の節約などのメリットに繋がることもあるだろう。私が耳にする「ビッグデータ技術の成功体験」の多くは、こうした情報である。だが、こうした技術だけではたいていの場合、ビジネスメリットに繋がらない。対処しきれない量のデータが存在する際に、適切なサンプリングさえすれば、必要な情報を得るためのコストが激減するのは80年前だろうが現代だろうが本質的には変わらない。にもかかわらず、ビッグデータに関心のあるビジネスマンは、しばしばビッグデータをビッグなままで扱うことにしか目が行かないのだ。ほんの1%やそこらの精度を改善することは、果たして数千万円も投資する価値のあるクリティカルな影響を持つのだろうか?必ずしも最初からすべての解析を全データで行なう必要はないのだ。解析はそれ自体価値があるものではなく、それを活かして何を行ない、どれだけの価値を得られそうなのかによって異なるのである。
第3章 誤差と因果関係が統計学のキモである
データ分析において重要なのは、「果たしてその解析はかけたコスト以上の利益を自社にもたらすような判断につながるのだろうか?」という視点だ。
具体的には、「ビジネスにおける具体的行動につながる」ということが重要である。
・データをビジネスに使うための「3つの問い」
【問1】何かの要因が変化すれば利益は向上するのか?
【問2】そうした変化を起こすような行動は実際に可能なのか?
【問3】変化を起こす行動が可能だとしてそのコストは利益を上回るのか?
この3つの問いに答えられた時点ではじめて「行動を起こすことで利益を向上させる」という見通しが立つのであり、そうでなければわざわざ統計解析に従って新たなアクションを取ろうとする意味はない。
だが、「十分なデータ」をもとに「適切な比較」を行なう、という統計的因果推論の基礎さえ身につければ、経験や勘を超えてビジネスを飛躍させる裏ワザはもっと簡単に見つかるはずなのだ。
実際のデータを使い、網羅的な比較を行なうことで「何となくわかっていたこと」は具体的な利益に繋がる数字とともに裏付けられ、「今一番何をすべきだろうか」という戦略目標が明らかになるのである。
具体的手法のうちの一つに、クロス集計表がある。そして、クロス集計表について「意味のある偏り」なのか、それとも「誤差でもこれぐらいの差は生じるのか」といったことを確かめる解析手法に「カイ二乗検定」というものがある。
この「実際には何の差もないのに誤差や偶然によってたまたまデータのような差(正確にはそれ以上に極端な差を含む)が生じる確率」のことを統計学の専門用語でp値という。
「適切な比較を行なうこと」、そして「ただの集計ではなくその誤差とp値についても明らかにすること」。この2点を意識しさえすれば、経験と勘を超えて裏ワザを見つけることが容易になる。
いざデータを分析しようとしたときにしばしば問題になるのは、「適切な比較」とは何か、あるいはもう少し具体的に言えば「いったい何と何を比較すればよいのか」という点である。私たちはいったいどのようなデータを比較し、その違いを生み出しうる要因を探し当てればよいのだろうか?その答えを一言で言えばごく簡単だ。「目指すゴールを達成したもの」と「そうでないもの」の違いを比較しさえすればいい。ここで重要になるのは「ここから何かわからないか」という漠然とした問いではなく、そのようなデータのうち何が、どのような関係で利益と繋がっているのかなのだ。
既存データから何らかの誤差とは考えにくい偏りを発見すれば、それは貴重な示唆に富む仮説となる。こうした有望な仮説を抽出するスピードと精度こそが現代における統計学の第一の意義であり、うだうだ会議で机上の空論を戦いあわせることなどよりもよほど有益だろう。
戦略目標につながる具体的統計学の適用法の1つは、「関連しそうな条件」を考えうる限り継続的に追跡調査し、統計学的な手法を用いて、少なくとも測定された条件については「フェアな比較」を行なうというものである。そしてもう1つは、解析ではなくそもそものデータの取り方の時点で「フェアに条件を揃える」というやり方である。
第4章 「ランダム化」という最強の武器
データの取り方自体を工夫すれば、あるいはより高度な解析手法を用いれば、完璧にとは言わないまでも何が原因で何が結果なのか、そしてその「原因」を制御することによって、どれだけ「結果」を左右することができるのかをかなりの部分明らかにすることができる。その具体的手法こそがランダム化比較実験である。
ランダム化比較実験がどれだけ強力か、本節で説明するその最も大きな理由は、「人間の制御しうる何物についても、その因果関係を分析できるから」である。
<「誤差」への3つのアプローチ>
1つは、実際のデータをまったく扱わず、ただ仮説やこういう事例がありましたという話だけをもとにして理論モデルを組み立てる、というやり方。
そして2つ目は、見かけ上「100回やって100回そうなる」という状態を示すために、うまくいった事例のみを結果として報告するやり方である。
そして最後の3つ目が、ランダム化を用いて因果関係を確率的に表現しようとするものである。
これは「諸条件をランダム化してしまえば、平均的に比較したい両グループ間で同じになる」という性質を活用している。
統計学は「最速かつ最善の答えを得るもの」として位置づけているが、ランダム化はまさにその中で最も強力な武器であると言える。
だが残念なことにこの武器はいつでも使えるわけではない。世の中にはランダム化を行なうこと自体が不可能な場合、行なうことが許されない場合、そして行なうこと自体は本来何の問題もないはずだが、やると明らかに大損をする場合、という3つの壁がある。1つめの壁は「現実」、2つ目の壁は「倫理」、そして3つ目の壁のことを「感情」と呼ぶこともできるだろう。以下、それぞれの壁について説明していきたい。
ランダム化に対する「現実」の壁とは、つまり「絶対的なサンプル数の制限」と「条件の制御不可能性」である。
「1回こっきりのチャンス」あるいは、あったとしてもせいぜい数回程度しかチャンスの与えられないもの自体を取り扱うことに対して、ランダム化しようがしまいが統計学は無力である。
そしてもう1つの「現実」の壁は、ランダム化しようにも条件を制御すること自体ができない、というものがある。
統計家たちの間で共有されている倫理的ガイドライン
ランダム化によって人為的にもたらされる、どれか1つまたはすべての介入が明らかに有害である(またはその可能性が高い)場合はダメ
仮にすべてが有害でなくても、明らかに不公平なレベルで「ものすごくいい」ものと、「それほどでもない」ものが存在していると事前にわかっている場合もダメ
科学的および倫理的な議論のうえで、どちらがよいか実際わかっていないからランダム化を行なうことが正当化されたとしても、「そういう運次第で自分の運命が左右されるのが何かイヤ」と実験に参加する人が思うことを止めることはできない。これが最後の「感情」の壁である。
第5章 ランダム化できなかったらどうするか?
適切なランダム化さえできれば、我々はこの世のありとあらゆる因果関係を科学的に検証し、利用することができる。だが、ランダム化による制御自体が不可能な場合、仮に可能であったとしても倫理的に許されない場合、そして理論上は倫理的な問題とならない場合であっても、関係者からの感情的な反発が予想される場合にはランダム化に基づく統計学の利用があまり適さない。
だが、ランダム化ができない場面において統計学が役立たずになるなんてことはもちろんない。
「ケースコントロール研究」と呼ばれるデータの取り方が重要になるのだ。
疫学におけるケースとは症例すなわち関心のある病気となった事例(患者)のこと。そしてコントロールとはその比較対照のことである。比較対照には「関心のある疾患とリスク要因の有無以外は条件がよく似た人」が選ばれる。「よく似た」の定義は研究によってさまざまだが、関心のあるリスク要因以外は考える限りすべての条件について同等であることが望ましい。性別・年代・社会階層・居住地域といったものについて、調査対象とした患者と同様の人間を集めて男女別や年代別で区切ったグループごとに比較(専門用語でこれを層別解析と呼ぶ)すれば、ランダム化をしなくても「フェアな比較」ができるというのである。
ランダム化比較実験を行なっていない解析では、いくら「同様と考えられるグループ内で層別解析をした」としても、厳密に同様な集団間での比較なんてあり得ないじゃないか、という限界がある。ランダム化を行なえば、どんな条件についても比較したい両グループ間で平均的には同様となる。どんな条件についても、というのは、その条件を測定しようが測定しまいが変わらないということだ。
だが、ケースコントロール研究ではどうだろうか。あくまで「同様」にできるのは、人為的に「同様」となるよう揃えた条件だけである。
<「揃えきれていない条件」にどこまでこだわるべきか>
すべてをランダム化をしていないため、いくら条件を揃えようが「揃えきれていない条件が存在している可能性」が捨てきれるわけではない。だが逆に、ではいったい何が揃えきれていない条件として存在しているのだろうか。科学的な厳密さにこだわれば「揃えきれていない条件」によって推定されたリスクが存在しない可能性はもちろんある。だが、厳密さに執着するために「大きな危険かもしれない」とわかっていることをあえて避けないというのも愚かな判断ではないだろうか。
疫学研究に反論したい人は、考えられる限り結果を歪めうる条件について指摘すればいい。そうすることによって、疫学研究が思わぬ落とし穴にはまって間違った結論を導く可能性は減らせる。だが、そうした指摘に対しても統計家がデータを揃えてきたのであれば、その結果は信頼したほうが現実的には有用である。
疫学研究から示されたリスクの大きさは「ケースコントロールはランダム化比較実験とあまり結果に差がない」である。そして、その理由としては「高度な統計手法によって、適切な条件の調整を行なうことができているから」である。
ランダム化比較実験がむずかしい状況なのであれば、比較的低予算でスピーディにデータが収集できる疫学的手法を用いることが現実的には有用であるという場面は、我々の社会に数多くあるのだろう。
<回帰分析とは何か>
ケースコントロール研究のようにわざわざデータの取り方を工夫しなくても、より高度な手法を用いれば可能な限り条件を揃えた「フェアな比較」が可能になる。そのための最も重要な枠組みの1つが回帰分析だ。
データ間の関係性を記述する、あるいは一方のデータから他方のデータを予測する数式を推定するのが回帰分析という考え方であり、こうした数式で記述される直線のことは回帰直線と呼ぶ。ただし、回帰分析によって得られた「最もそれらしい予測式」を得ただけで満足してはいけない。なぜならその予測式は最もデータとの誤差を最小化するように得られたものではあるが、依然として誤差が存在することに変わりはないのだ。
ではどのように考えればよいのだろうか?
得られた回帰係数自体にバラつきが存在していると考える。すなわち、仮に今後100回「たまたま得られたデータ」から回帰係数を計算したとしたら、「比較的大きな値となることもあれば小さな値となることもある」というバラつきを考慮しなければいけないのだ。
「無制限にデータを得ればわかるはずの真に知りたい値」を真値と呼び、たまたま得られたデータから計算された統計量がどの程度の誤差で真値を推定しているかを数学的に整理することで、無限にデータを集めることなく適切な判断が下せるという考え方が示されている。
現実のデータから得られた回帰係数などの統計量はあくまでこの真値に対する妥当な推定値であり、単に一番もっともらしい値を推定するだけでなく、それが真値に対してどの程度の誤差を持っているかを考えれば、少なくとも間違った判断を犯すリスクは減らすことができる。
回帰係数の推定値:切片・傾き(x)ともにデータから算出された値だがあくまでデータに基づき「真値」を推定した結果だということに注意。
標準誤差:推定値の誤差の大きさ。回帰係数の推定値と比べて大きければあまり推定値は信頼できないが、この値自体を問題にするよりは後述の信頼区間で考えたほうがいい。
95%信頼区間:「回帰係数が0」の場合だけでなくさまざまな回帰係数を想定して、「p値が5%以下になる真値としてあり得ない値」とはならない範囲。「ほぼこの範囲内に真値があると考えて間違いない」と考えて大丈夫。
p値:仮に回帰係数が0だった場合にデータのバラつきのせいだけでこれぐらいの回帰係数が推定されてしまう確率。やはり慣例的には5%を下回ると「さすがに回帰係数0と考えるのはキビシイ」と判断される。
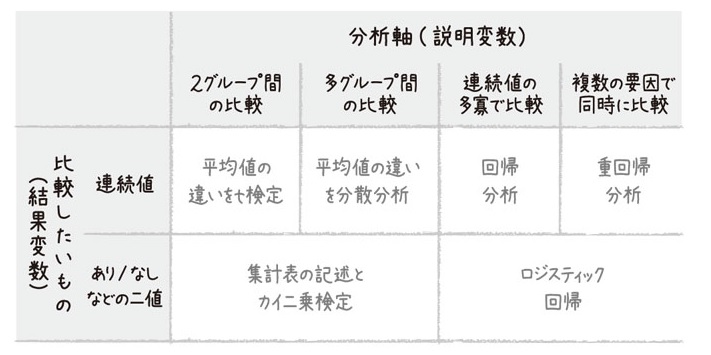
重回帰分析は、説明変数すなわち予測したい結果に影響する要因が複数ある状況へ拡張された回帰分析であり、これも統計学において重要な「フェアな比較」を行なううえで重要な役割を果たす統計解析手法である。
全集団同士での単純比較は、その内訳となる小集団同士との比較の結果と矛盾することもある、だから疫学のような観察研究では条件を揃える必要があった。結果に影響しうるような条件について「同様の小集団」同士で比較すれば、この矛盾は避けられるはずだ。この考え方は基本的に正しい。だが、「結果に影響しうるような条件」が多くなれば、このようなやり方は徐々にうまくいかなくなってくるのである。
こうした問題に対して重回帰分析は威力を発揮する。回帰係数と複数の回帰係数を同時に推定するのが重回帰分析である。これが重回帰分析によってフェアな比較が行なわれたということである。こうしたやり方であれば、多少条件が増えたとしても莫大な数の層に分ける必要はない。複数の回帰係数は「お互いに相乗効果がなかったとすれば」という仮定のもと、説明変数が結果変数にどの程度の影響を与えるかを示している。
重回帰分析は結果変数が連続値である場合にしか使うことはできないが、フラミンガム研究において、それをさらに拡張したロジスティック回帰というものが発明されている。二値の結果変数に対して、重回帰分析と同様にさまざまな説明変数が与える影響をフェアに分析しようと、この手法は生みだされた。
もともと0か1かという二値の結果変数を変換し、連続的な変数として扱うことで重回帰分析を行なえるようにした、というのがロジスティック回帰の大まかな考え方である。
ロジスティック回帰では、回帰係数をオッズ比つまり「約何倍そうなりやすいか」で示すということさえ知っていれば、結果の理解に問題はない。知っていれば、結果の理解に問題はないだろう(なお正確には、推定された対数オッズ比を変換しオッズ比の形で結果を示す)。重回帰分析と同様に、回帰係数の推定値、標準誤差と信頼区間、それにp値というのが読み取るべき値であり、その回帰係数の結果の読み方だけが少し異なるのだ。
重回帰分析やロジスティック回帰のような回帰モデルは、データの関連性を見るうえで現在最も頻繁に用いられる便利な手法である。ある。しかしながら、回帰モデルによって必ず因果関係が適切に推定できるかというと、そういうわけにもいかない。どこまでのことが言えてどういった点に注意すべきか、ということがわかってこそ、誤りのないデータの解釈ができるようになる。
回帰モデルを使ううえで重要な注意点の1つが、このような交互作用が本当に存在していないかというものである。つまり、それぞれが連続値だろうが、ダミー変数だろうが、2つの説明変数それぞれの回帰係数だけでなく、2つの変数を掛けあわせた新しい説明変数(これを交互作用項と呼ぶ)を作り、その回帰係数についても同時に推定する、というだけでこの交互作用の影響は推定することができるのである。
傾向スコアあるいはプロペンシティスコアと呼ばれる手法がある。この方法は主に疫学分野でランダム化が不可能あるいは困難な因果関係の特定に重宝されてきた。具体的には、傾向スコアが同様の集団、つまり年齢や居住地域、職業などの条件から推定された「喫煙するだろう」という確率が同じ集団同士で比較すれば、「その他の条件」と「喫煙の有無」の関連性が「喫煙の有無」と「肺がん」の関連性を歪めることはなくなるのだ。
第6章 統計家たちの仁義なき戦い
統計学がITとの融合によってその影響力を爆発的に拡大させた、というのはすでに述べたところだが、その結果として生じたのがデータマイニングと呼ばれる研究領域との接触である。
シンプルな計算だけで何かしら関連性のある商品を見つけられる、というのがバスケット分析の利点であるが、統計学を知っていれば「もっとよいやり方があるではないか」とすぐに気づく。こうした集計表の相関を分析するとき、統計学ではカイ二乗検定の計算のもととなっているカイ二乗値を用いる。
カイ二乗値を使えば「推定値の誤差」のようなものを考慮することができるため、支持度のような指標を用いることもなく、カイ二乗値が大きければそれは自動的に改善度だって大きいのである。なお、それぞれの商品の販売有無という二値変数間で、カイ二乗値の大きい組み合せ選ぶことと相関係数の絶対値が大きいものを選ぶことは、まったく同じ意味を持っている。
一方、ニューラルネットワークやサポートベクターマシンという手法を用いれば、曲線的な関係性や交互作用も含め、最も識別力が高いと考えられる分類を行なうことができる。たとえばニューラルネットワークでは入力データから「中間層」にあたる値を生み出す。中間層の数や中間層に含まれる変数の数はいくつに設定してもいいが、入力データからどの項目を用いて、それぞれどのような重みで中間層が算出されるか、というのは自動的に計算される。この楕円と矢印が神経細胞であるニューロンとその間の繋がりを模しているというのである。
<「予測」に役立つデータマイニング>
ただし、そのメリットを享受できるのはあくまで分類や予測だけが目的である場合、である。
ニューラルネットワークの複雑な矢印がそれぞれどの程度の関連性を示しているか、あるいはサポートベクターマシンの曲線がどのような式で表されるか、といった結果は人間の目でわかりやすいものにはなっていない。そうすると、いくら予測の精度が高くても、「では実際にどうすればいいのか」というアクションが見えてこないということになる。が「途中の計算はよくわかりませんが顧客の購買金額を予測できるプログラムが書けました」というのではどうしようもないのである。予測、それ自体がゴールなのであればデータマイニングは有効である。しかしながら予測自体ではなく、予測モデルから今後何をすべきかを議論したいのであれば、回帰モデルのほうが役に立つ。こうした違いを理解したうえで適切な手法を選び分けることが、21世紀の統計家には求められるのである。