ゲート付き回帰ユニット(GRU:Gated Recurrent Unit)は2014年に提案されたニューラルネットワークです。LSTMニューラルネットワークと比較すると、非常によく似てはいますが、出力に内部状態を結合する際、たった2つのゲートしか必要としません。
GRUの特徴
下図は、GRUニューラルネットワークの計算を表しています。GRUでは、明示的な内部状態の転移(Transference)は必要ありません。なぜなら、内部状態はベクトル\(y_t\)へ結合されるからです。ステップ\(t\)で、GRUネットワークは、更新ゲート(Update Gate)と呼ばれるバイナリベクトル\(z_t\)と、リセットゲート(Reset Gate)と呼ばれるバイナリベクトル\(r_t\)を計算します。それぞれのゲートは、更新ゲート層とリセットゲート層で計算されることになります。
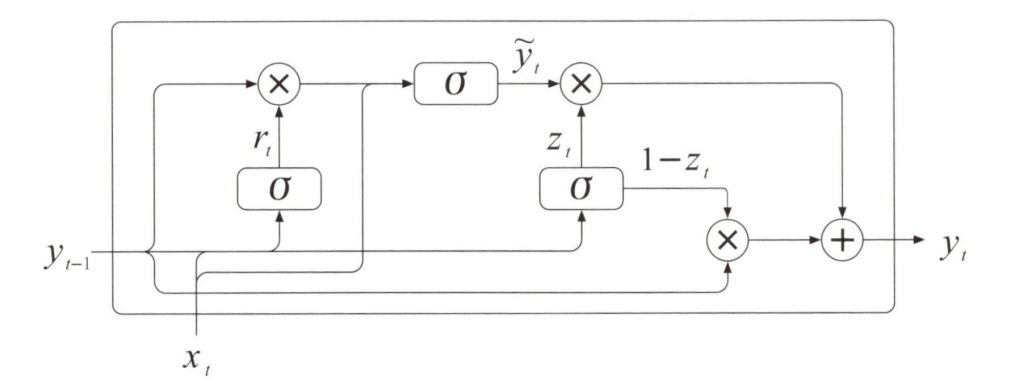
GRUニューラルネットワークの計算
・更新ゲート
更新ゲートは次式で表されるように、2つの要素ごとの積による新しい値でアップデートされる出力\(y\)を入力とします。例えば、もし\(z_t\)がバイナリベクトル(1,0,0,1)だとすると、要素ごとの積\((1-z_t)✕y_{t-1}\)により、1番目の要素と4番目の要素が0になります。これは、\(y_{t-1}\)の一部の要素がGRUによって忘れ去られたという意味です。\(y_{t-1}\)の残りの要素が記憶として残ります。反対に、要素ごとの積\(z_t✕y_t\)により、\(y\)の1番目と4番目の新しい値が保持されます。そして、その他の要素については無視されます。
\(y_t=(1-z_t) ✕ y_{t-1}+z_t ✕ \vec{ y_t } \tag{1} \)
・リセットゲート
リセットゲート\(r_t\)は次式で表されるように、\(y_t\)の新しい値を計算するために、GRUが\(y_{r-1}\)の要素を全結合層経与えて、ゼロにリセットします、例えば、もし\(r_t\)がバイナリベクトル(0,0,1,1)だとすると、要素ごとの積 \(r_t✕y_{t-1}\)により、\(y_{t-1}\)の1番目の要素と2番目の要素がゼロにリセットされますが、\(y_t\)の計算には影響しません。このとき、残りの\(y_{t-1}\)の残りの要素についても触れることはありません。
\(\begin{eqnarray}
\vec{ y_t }
=σ(W_y✕[r_t✕y_{t-1},x_t]) \tag{2}
\end{eqnarray}
\)
更新ゲート\(z_t\)の計算とリセットゲート\(r_t\)は次式に示すとおり、\(W_z\)と\(W_r\)の重みパラメータが分けられていることを除いて、よく似ています。どちらのゲートも、入力ベクトル\(x_t\)を前ステップの出力ベクトル\(y_{t-1}\)に結合して長いベクトルを生成します。この長いベクトルと重みパラメータの行列をかけ合わせて、その計算結果を\(σ\)関数ヘ代入し、2値の値を持つゲートのバイナリベクトリを得ます。
\(\begin{eqnarray}
\vec{ z_t }
=σ(W_z✕[y_{t-1},x_t]) \tag{3}
\end{eqnarray}
\) \(
\begin{eqnarray}
\vec{ r_t }
=σ(W_r✕[y_{t-1},x_t]) \tag{4}
\end{eqnarray}
\)
GRUニューラルネットワークには、\(W_z\),\(W_r\),\(W_y\)の3つの重みパラメータ行列が必要となります。
LSTMニューラルネットワークでは\(W_f\),\(W_i\),\(W_ο\),\(W_h\)のような4つの重みパラメータ行列が必要だったので、それよりシンプルです。
より効率的に記憶できる
GRUの更新ゲートは、LSTMの忘却ゲートと入力ゲートに比べてシンプルに動作します。GRUの出力のうちの1つの古い値を覚えておくか、新しい値で置き換えるかについて考えます。更新ゲート\(z_t\)が記憶の一部を更新せず、記憶の一部については触れないようにすることで、LSTMのように、長期のステップにわたる記憶を行えるため、GRUは単純なRNNより効率的な記憶のメカニズムとなっています。
GRUニューラルネットワークにおいて奇妙な点があるとするなら、内部状態と出力を結合する部分です。単純なRNNとLSTMではどちらも内部状態\(h\)が出力\(y\)と別れています。しかしながら、GRUニューラルネットワークでは、出力yからの1本のパスしかありません。これらを比較すると、GRUの内部状態は出力\(y\)であると考えることが出来、単に\(y\)を他の全結合層へ結合するだけで出力が得られます。