階層間のニューロンが全て結合されている層を全結合層と呼びます。以前の記事で多層パーセプトロンと呼んでいたものと同じです。全結合層を使うと、入力データをいくつかのパターンに分類することが出来ます。
全結合層の処理
深層畳み込みニューラルネットワークではよく、出力層として全結合層をネットワークの末尾に連結することがあります。これは、いくつかの畳み込み層によって画像の特徴が要約された後に、分類や推測を行うためです。手書き数字画像の認識などでよく使われます。
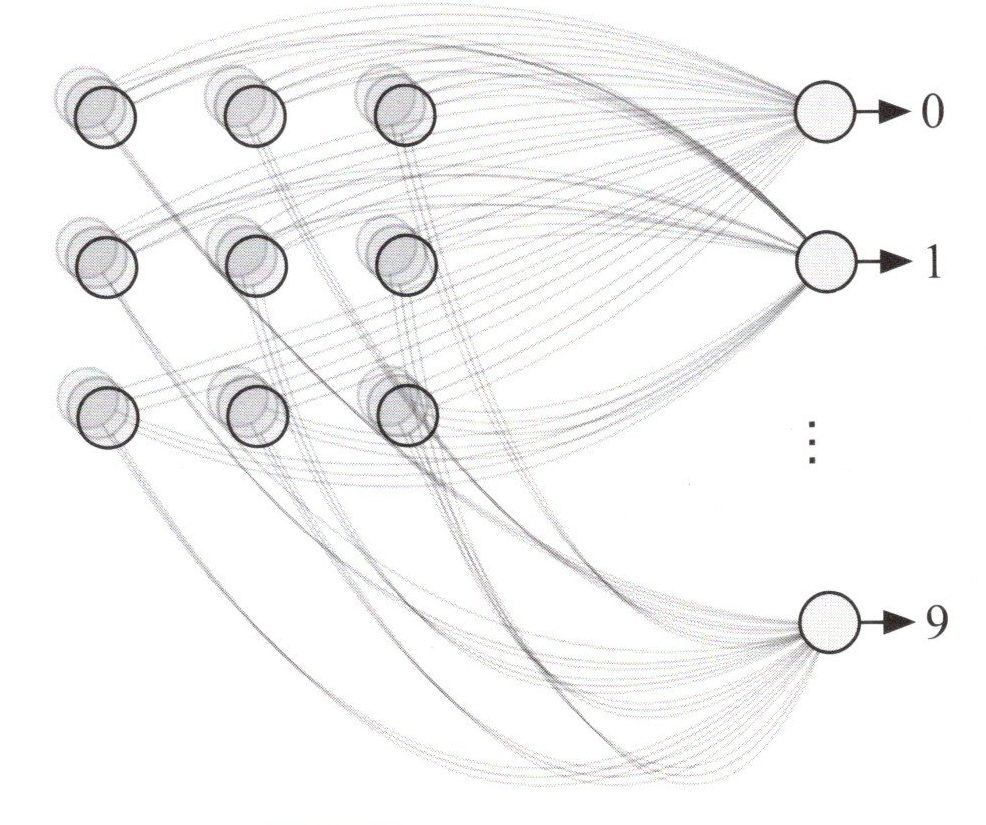
全結合層
上図は全結合層を表していて、それぞれのニューロンが全ての出力データ\(z_1\)に対応し、\(i \in 0,…,9\)は全結合層の各ニューロンのインデックスを表します。入力画像が手書きの数字画像の場合、0~9の特定の数値である確率が、入力\(x\)と重み\(w\)から\(wsm\)演算子によって計算されます。
\(\begin{eqnarray}
z_i=wsm(w_i,x)
\tag{1}
\end{eqnarray}
\)
ここで、確率の計算は\(softmap\)活性化関数によって行われます。これは10個全てのニューロンによる\(wsm\)の計算結果を、次式でかけ合わせたものです。
\(\begin{eqnarray}
y_i=\frac{exp(z_i)}{\sum_{j=0}^{9}{exp(z_j)}} \tag{2}
\end{eqnarray}
\)
全結合層の出力は、数字を意味するクラスを表す確率ベクトルになります。この確率ベクトルは、例えば\(y\)=(0.01,0.01,0.01,0.01,0.01,0.91,0.01,0.01,0.01,0.01)のようになります。
この確率ベクトルの例では、6番目(\(i=5\))の値の確率が0.91(\(y_5=0.91\))で最高値のため、手書き数字クラスのラベルとして「5」を付与します。この様に、出力結果を3つ以上のクラスに分類する問題は、多値分類問題または多クラス分類問題(Multi-class Classification Problem)と呼ばれています。
全結合層の修正
目的が異なる場合は、全結合層を修正することも出来ます。例えば、1枚の画像の中に人間がいるかどうかを判定したい場合は、出力層は1個のニューロンで事足ります。まず畳み込みニューロンで1枚の画像の中の人間の抽象的な特徴を出力データとして表現し、この出力データを出力層野入力として、\(wsm\)演算を計算します。
\(\begin{eqnarray}
z=
wsm(w,x) \tag{3}
\end{eqnarray}
\)
この式ではシグモイド(sigmoid)活性化関数を使って、画像の中に人間が見えるかどうかの確率を計算しています。
\(\begin{eqnarray}
y
=
\frac{1}{1+e^{-z}} \tag{4}
\end{eqnarray}
\)
シグモイド関数の出力は、0より大きく1より小さい値の範囲(0,1)となります。この値を閾値(threshold)と比較して、出力のクラスのレベルを1(画像に人間が見える)または0(画像に人間が見えない)とします。例えば閾値を0.5とし、もしy≧0.5なら1、それ以外(y<0.5)なら0のようにします。このような2値のクラスに分ける問題は、二値分類問題(Binary Classification Problem)と呼ばれます。
より複雑な判断をしたいとき
さらに複雑なケースとして、例えば人間、猫、犬、その他いろいろな家具など、多くのオブジェクトを含む画像があったとき、これらのオブジェクトに該当するクラスが、この画像の中に存在するかどうかを判断したいことがあります。そのようなときには、畳み込みニューロンに人間、猫、犬、その他の家具を学習させて、抽象的な特徴に変換し、複数のニューロンに与えます。複数のニューロンは、それぞれ単独のニューロンとして機能し、(0,1)の範囲で確率を出力します。この確率値を基にして特定のクラスに含まれるかどうかを予測し、ラベル付けを行います。これは前述した二値分類問題を多値分類問題に拡張したものと言えます。また、この問題は、一度に複数のラベルを付与できるので、多クラスマルチラベル分類問題(Multi-Class Multi-Label Classification Probrem)とも呼ばれます。