時々、入力データに対してもっと積極的に受容野を動かしたいときがあります。これは、畳み込みニューロンの受容野の大きさでは対応できない大きな画像が与えられた場合などです。
ストライドとは
畳み込みニューロンの移動距離はストライド(stride)と呼ばれます。前の記事の例では畳み込みの距離は1でした。下図はストライドを2として、\(4✕4\)の大きな受容野で\(6✕6\)の入力データを畳み込む処理の様子です。ニューロンは入力データの上部を2歩だけスライドできます。さらに入力データの下部を2歩スライド出来ます。この結果、出力データの形は\(2✕2\)まで集約されます。
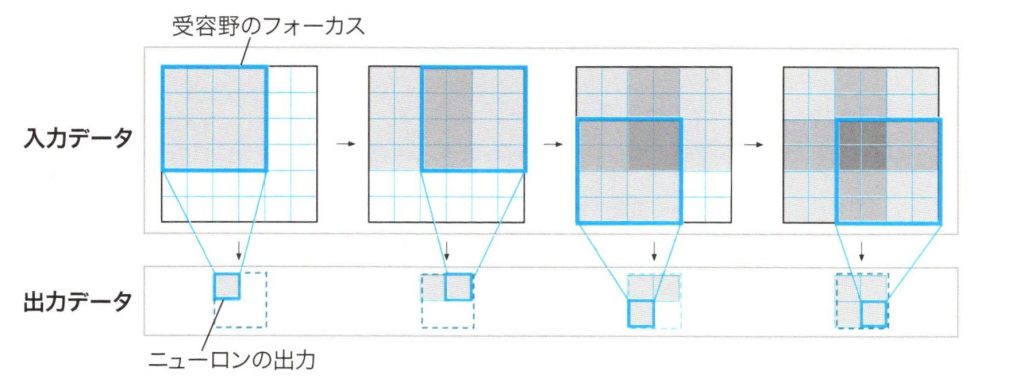
2歩ずつ進める畳み込み処理
一般的に、1枚の入力データの形が\(W✕W\)、畳み込みニューロンの受容野が\(F✕F\)、ストライドがSで与えられた時、出力データの形は、\((W-F)/S+1\)で幅と長さが計算できます。
ゼロパディングの利用
畳み込み演算では、境界部分の情報を保存するためにゼロパディングも利用できます。下図は幅1のゼロパディング、ストライド2の畳み込みの様子です。
\(W✕W\)の形状の1枚の入力データ、\(F✕F\)の形状の畳み込みニューロンの受容野、幅\(P\)のゼロパディング、ストライド\(S\)が与えられた時、出力データの形状は、\((W-F+2P)/S+1\)で幅と長さが計算できます。
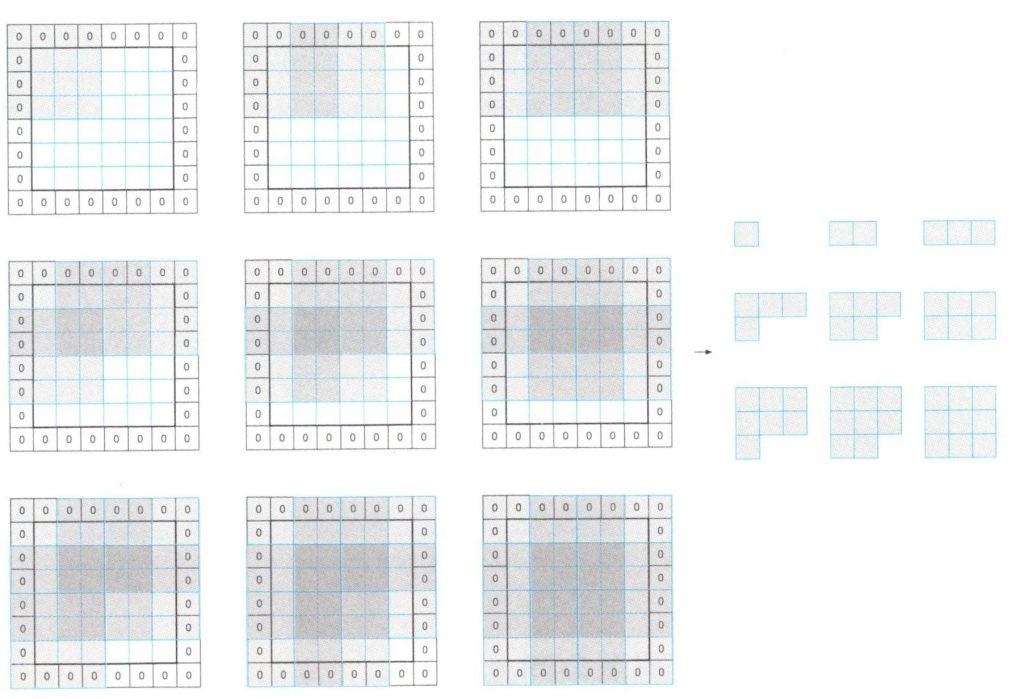
ゼロパディング1、ストライド2の畳み込み処理