本記事では、世代交代モデルについて最初に触れた後に、遺伝的アルゴリズムが抱えている問題点(限界)、遺伝的アルゴリズムの要約について記載していきます。
New Generation Alternation Model(世代交代モデル)
世代交代モデルには2つの基本的方式があります。それぞれについて以下に記載します。
・離散世代モデル(discrete generation model)
全ての個体が一斉に繁殖を行い、現世代集合全体が次世代集合に置き換えられるモデルです。特徴として、世代間における個体のオーバーラップが存在しないことが挙げられます。
<単純GAモデル>
ルーレット選択と交叉・突然変異を用いて、親世代と同数の子個体を生成し、子個体のみを次世代として
残すモデルです。このモデルのデメリットとして、初期収束による局所解の発生や、進化的停滞が起こりや
すいことが挙げられます。
・連続世代モデル(continuous generation model)
現在の世代のうち一定の割合の個体だけを入れ替え、残りはそのまま次世代に残すモデルです。
下記の3つの基本的なモデルがあります。
<世代ギャップ>
離散世代モデルにおいて、各世代の個体のうち次世代と入れ替えるものの割合のことです。
<定常状態モデル>
1世代につき1組(2個)の親個体から子個体を生成し、現世代のうち最も適応度の低い個体と入れ替えるモデ
ルです。
<世代間最小ギャップモデル>
ランダムに選択された親個体2個と、そこから作られる子個体2個を1つの「家族」とします。その家族の
中でエリート選択とルーレット選択により、2個体を次世代に残します。これを家族の数だけ行うモデルで
す。親子個体の選択を適応度を考慮せずにランダムに行うため、多様性維持に優れており、初期収束が起こ
りにくいという特徴があります。また、家族内で選択を行うため、計算負荷が軽く、並列計算への適応もし
やすい、というメリットもあります。
遺伝的アルゴリズムが抱えている問題点
遺伝的アルゴリズムのknown issueとして、「初期収束」と「ヒッチハイキング」が挙げられます。>
<初期収束>
最初の方の世代で「偶然」他の個体よりも適応度が圧倒的に高い個体が生じた場合、その個体の遺伝子が集団中に爆発的に増えて、探索がかなり早い段階で収束してしまう現象のこと。
<初期収束への対策>
各パラメータを繰り返し設定し直してトライするしかない。
具体的には、下記のような対策が挙げられます。
・集団数を増やす
・ランキングの選択確率を変更する
・トーナメントサイズを縮小する
・突然変異率を増やす
・適用する問題に対して効果的となるように、突然変異操作を変更する
など。
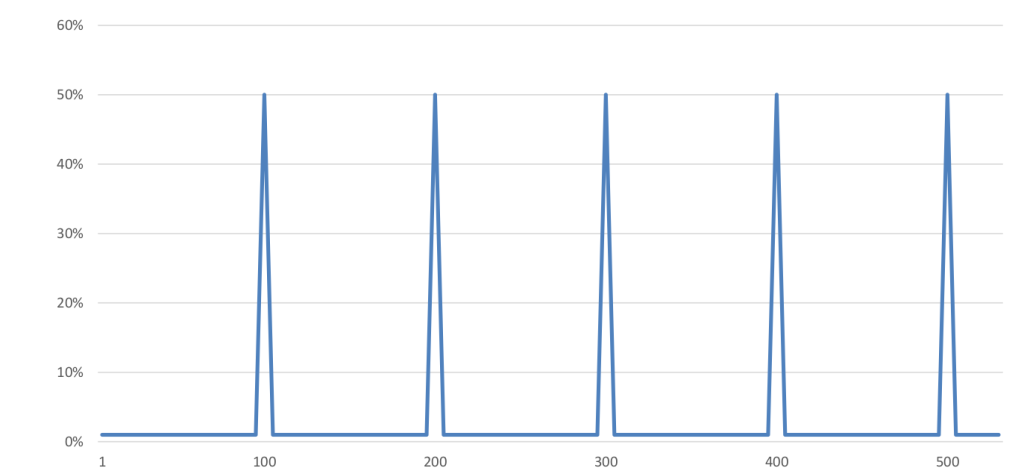
他の対策としては、大変異が挙げられます。大変異とは、予め定めた条件に応じて、特定の世代においてのみ突然変異率を急激に高める方法のことです。これは、自然感における環境の激変(隕石の衝突など)に相当します。
[大変異の設定例]
例えば、通常1%で設定した突然変異率を、100で割り切れる世代のみ50%とする。
さらに他の方法としては、適応変異が挙げられます。
<適応変異とは>
親個体間の不一致度合い(ハミング距離)に応じて、生成された子個体の突然変異率を変化させることです。
例えば・・・
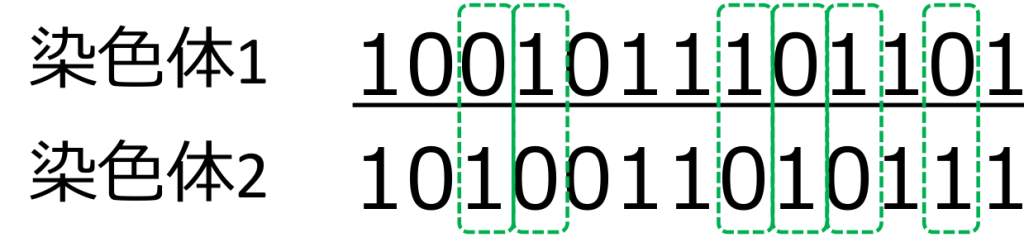
ハミング距離=6 → 突然変異率=1% と設定する
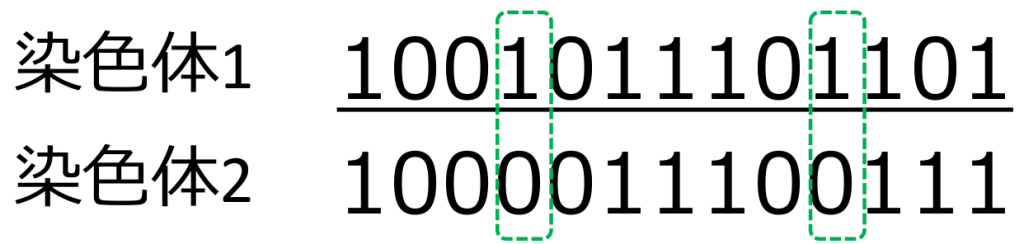
ハミング距離=2 → 突然変異率=8% とする
このようなイメージです。
<ヒッチハイキング>
遺伝子操作時に最適解と一致しない遺伝子が混入してしまうことによって、最適解の生成を妨げる現象のこと。二点交叉で発生しやすい事象です。
最適解=…11110100000…
に対して、
親1=….11110000000…
親2=….11111110000…
が交差して最適解を得られる確率/(P/)は、二点交叉の場合、
\begin{eqnarray}
P
=
\frac{2}{L(L-1)} \tag{1}
\end{eqnarray}
\)
(L=遺伝子長)
遺伝子長が増加するにつれて、加速度的に最適解を得られる確率が低下します。
しかし、一様交叉であれば、
\begin{eqnarray}
P=
\frac{2}{2³}=\frac{1}{4} \tag{2}
\end{eqnarray}
\)
となり、遺伝子長に依存しません。
(ヒッチハイキングの対策として、一様交叉を採用するのがベスト、ということです。)
要約
遺伝的アルゴリズム(Genetic Algorithm)とは、生物の遺伝を模したアルゴリズムであり、適者生存による自然淘汰で最適解を探索することが出来ます。また、大きなメリットとして、対象となる問題に関する数学的な知識がない場合でも適用が可能な点が挙げられます。
問題の最適解を導出するには、性質に適したエンコーディングと交叉方法を選ぶことが重要になってきます。組み合わせの増加などにより指数関数的に複雑さが増加する問題に対しても、線形的な時間増加で探索を行うことが出来ます。
局所最適解への収束を防ぐために、状態に応じて突然変異の方法や確率、トーナメントサイズなどのパラメータを変えることも必要です。