畳み込みネットワークには、その性能を向上させるための多くのテクニックが考案されえています。最も重要なものの1つは、いくつかの連結された畳み込みReUL層の間にプーリング層(Pooling Layer)を挿入することです。プーリング層は、畳み込み層から出力される幅と長さを削減することで知られています。
→Q:なぜ出力される幅と長さを削減するの?
A:情報を厳選することで、認識率を向上することが出来るからです。
プーリング層による処理
下図は、どのようにしてプーリング層が、畳み込み層の出力データの形を縮小するのかを図持しています。プーリング層は、畳み込み層から\(6✕6✕3\)の形の出力データを受け付け、
①まずは、\(6✕6\)の2次元のデータとして3枚にスライスします。
②次に、3枚の\(6✕6\)のデータをそれぞれ、重複なしで小さな\(2✕2\)の領域ごとに切り分けます。
③さらに、\(2✕2\)の領域の4つの値のうち、最大値を選びます。
④最後に、その最大値は、\(2✕2\)の領域の代表値として、その領域の代わりにセットされ、\(3✕3\)のデータになります。
プーリング層が\(2✕2\)の領域から1この値を選ぶため、入力データは幅と長さが縮小され、\(3✕3✕3\)の形の出力データとなりますが、深さ方向には変化はありません。
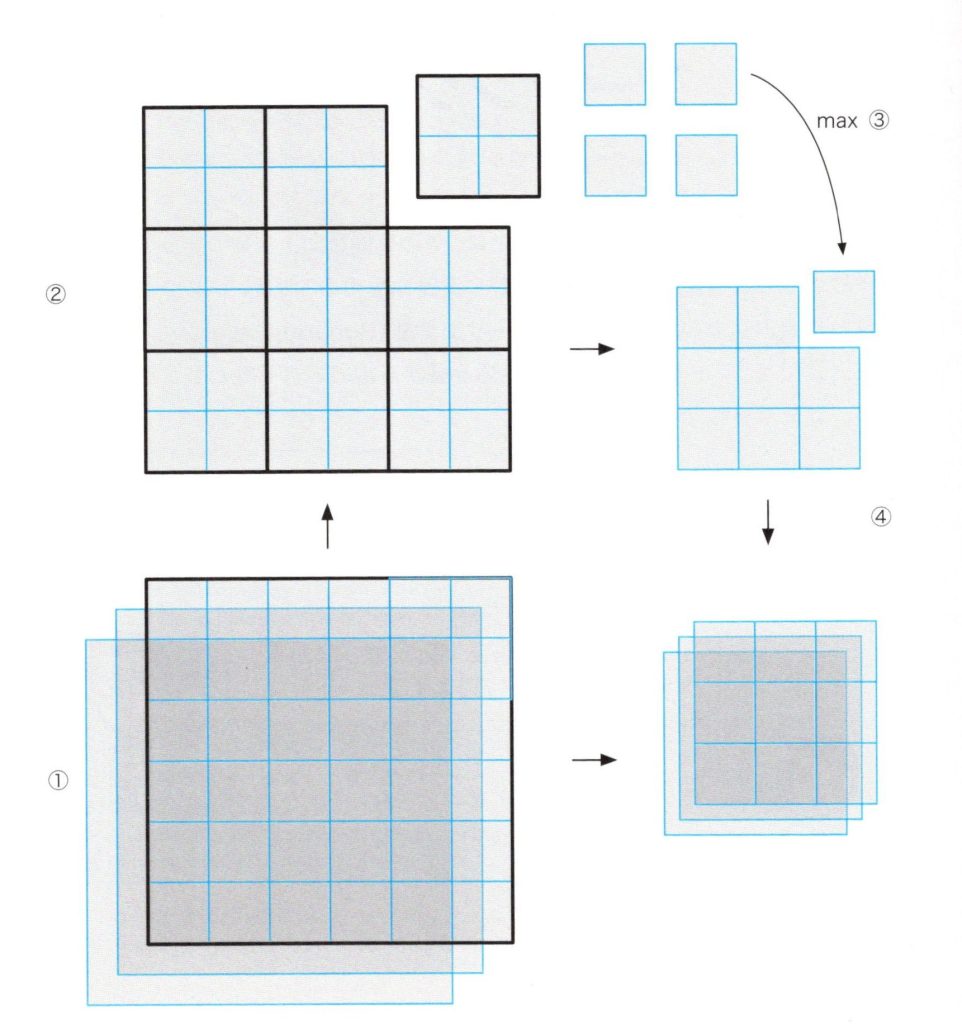
プーリング処理
プーリング層の利点と注意点
出力データが縮小されることは、後段の畳み込み層のニューロンが扱うデータを小さくするため、より少ない畳み込み層によって入力データの全体を見渡すことが出来るというメリットがあります。畳み込みニューラルネットワークへのプーリング層の挿入は、パラメータ数を減らし、過学習問題を制御することで、モデルの学習性能を改善します。
プーリング層は、出力データの小さな領域ごとに最大値を選ぶため、最大プーリング(Max Pooling)とも呼ばれます。最大プーリングの他にも、平均プーリング(Average Pooling)やL2- ノルムブーリング(L2-norm Pooling)といったプーリング手法もありますが、最大プーリングはシンプルで効率的なので、実際のアプリケーションでよく使われます。
<注意点>
本記事の例ではs、プーリングの戦略を広く利用しますが、改良の余地があります。一般的な改良方法は、プーリングの対象となる領域のサイズを大きくすることです。例えば、\(2✕2\)を\(3✕3\)とします。このとき、プーリング層は\(3✕3\)の範囲の9個の値の中から最大の値を選び、これ以外の8個の値は出力データから削除されます。
なお、プーリング戦略は比較的小さい入力データに対してはやりすぎてしまい、大事な情報が抜け落ちてしまうこともあります。このような場合には、例えば\(3✕3\)の領域に対して重複1とするなど、小さな重複(overlapping)を許したプーリング層にすることで入力データの情報の損失を減らすことが出来ます。しかしながら、プーリングの対象の幅が3よりも大きい値は、実際のアプリケーションではレアケースのようです。