本記事では、畳み込み演算の2つの副作用について説明します。1つは、出力される形の収縮と、もう1つは入力値に対するボーダーラインに達しなかった情報の損失です。これらの問題について考えてみます。
収縮する出力の形
前の記事では、畳み込みニューロンが、\(W✕W\)の形の入力画像の左から右、上から下へフォーカスをスライドしながら\(F✕F\)の形に受容野から入力し、\((W-F+1)✕(W-F+1)\)の形の出力を生成しました。深層畳み込みネットワークで多層に畳み込み演算を行うことで、出力の形を素早く収縮させることが出来ます。この様子を下図で示します。
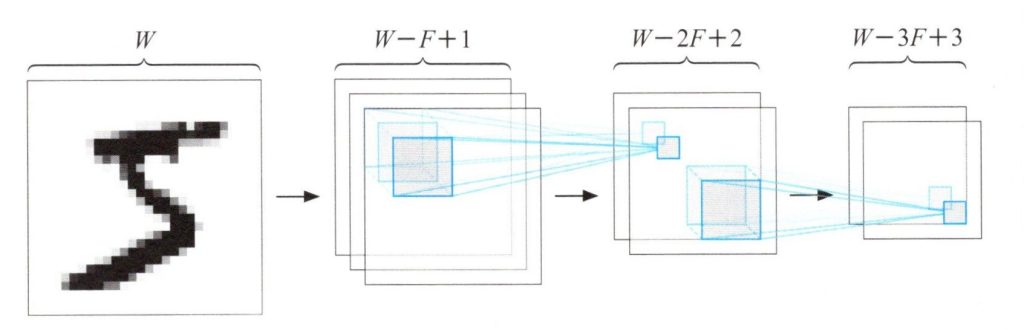
連続する畳み込み演算による出力の収縮
入力データの周辺情報の損失
出力の形状を収縮する処理により、入力データの周辺部分の情報の損失という別の問題が浮上します。畳み込みニューロンは、入力データ上の局所的な領域に対して、受容野を機械的に移動させます。しかしながら、入力データを領域ごとに見ると、受容野が移動してくる回数に大きな違いがあります。下図は、その回数の多さを色の濃さで表しています。入力データは、\(6✕6\)の形状で\(3✕3\)の受容野野畳み込みニューロンによって畳み込み処理が行われます。毎回、ニューロンは\(3✕3\)の領域をチェックしていますが、ある領域ではやや影がかかっています、入力画像の緑、周辺部分の影は中心部分と比べて明るくなっています。そのため、畳み込みニューロンが情報を入力データから次の階層へ受け渡す時、入力データの中心部よりも周辺部分のほうが少ない情報量となってしまいます。
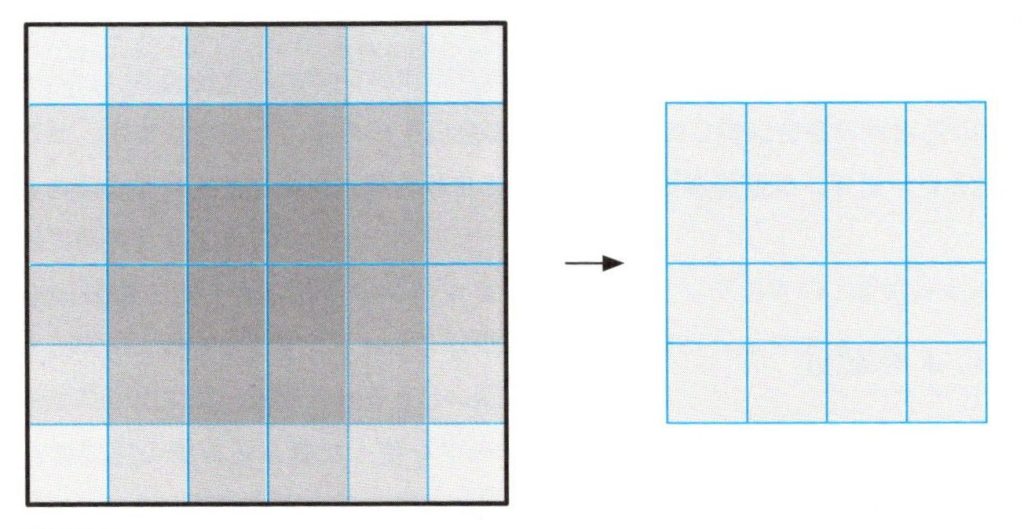
入力データの周辺部分は中心部分より学習されにくい
ゼロパディング
この問題を解決するため、シンプルな分散を導入します。ゼロパディング(zero-padding)による畳み込みの手法です。基本的なアイデアとしては、入力データの境界線の外側にデータを追加することで、元の入力データの境界部分に対する処理を強化しよう、という手法です。
下図では、空の部分に0の値を入れた状態を表しています。\(3✕3\)形状の受容野の畳み込みニューロンに対して、入力データにサイズ1の空の境界線を追加するため、入力データの形は\(6✕6\)から\(8✕8\)に拡張されます。このとき、\(8✕8\)の入力データ上をニューロンの受容野でスライドさせながら畳み込み演算を行うと、\(6✕6\)の出力データが得られます。
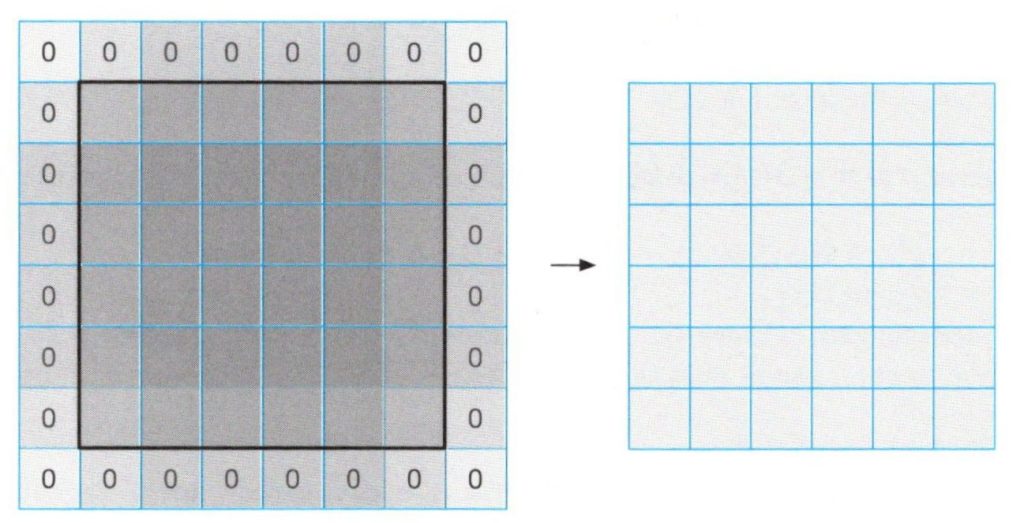
ゼロパディングによる畳み込み
入力データの幅と長さが増加したことで、元の入力データの形と同じ形の出力データとなります。重要なことは、畳み込みニューロンが、元の入力データの線の部分を中心の部分と同じ様に取り扱える様になったということです。(学習の偏りが少なくなった)
一般化していうと、\(F✕F\)の形状の受容野を持つ畳込みニューロンに対して\((F-1)/2\)の幅の空の境界線を追加すれば、畳み込みニューロンは、元の入力データと同じ傾向を持つ出力データを生成できます。例えば、\(3✕3\)形状の受容野が幅1の空の境界線で余白を埋める(パディング)ことになり、\(5✕5\)形状の受容野の場合は幅2の空の境界線で余白を埋めることになります。ゼロパディングによる畳み込みは、近年、深層畳み込みニューラルネットワークをデザインする際によく用いられます。