ここまでで、非常にシンプルな畳み込みニューラルネットワーク(CNN)について説明してきました。ネットワークを構成するたった1つのニューロンが、四角い領域の入力を受け取って、それに類似する四角い出力が出来るように学習しました。このシンプルなCNNによって、入力画像の中の各領域に、学習したパターンがあるかどうかをチェック出来るようになります。
異なるパターンを認識させるには
これまで解説したように1つのニューロンで学習できるパターンは1つのみです。実際の画像を分類しようとすると、各領域の異なるパターンを見つける必要があります。このため、もっと多くのニューロンをネットワークに追加する必要があります。このような多くのニューロンによって構成される層のことを、畳み込み層といいます。下図の(a)は、3つのニューロンを使った畳み込み層の畳み込み演算の様子です。さらに下図の(b)は、実際の入力画像に対して3つのニューロンを持つ畳み込み層が、畳み込み演算した結果を3枚の出力データとして出力する様子です。
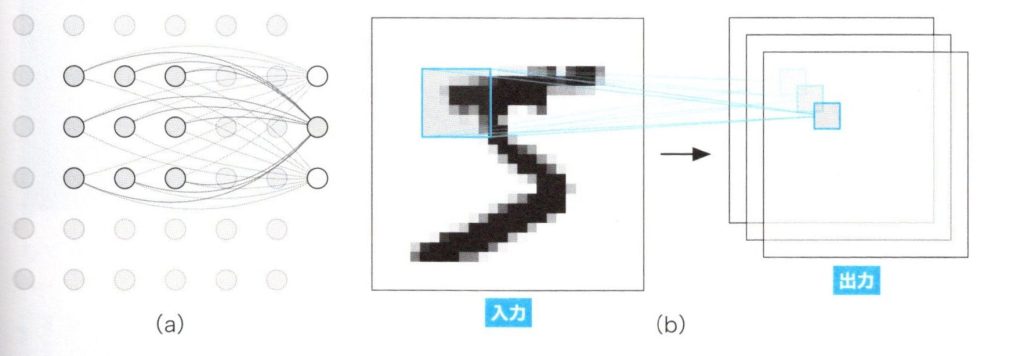
畳み込み層の畳み込み演算
上図の(a)では、3つのニューロンが同じ形状の受容野を持っていて、入力画像の同じ領域にフォーカスしています。しかしながら、局所的なニューロンの出力を次式のように定義し、これらの持つ重み\(w_0\),\(w_1\),\(w_2\)に異なる値をセットすることで、異なるパターンとして認識することが可能です。
$$
\begin{eqnarray}
y^0&=&wsm({w^0},x)=\displaystyle \sum_{i,j} w_{ij}^0{・}x_{ij} \qquad(1) \\\\
y^1&=&wsm({w^1},x)=\displaystyle \sum_{i,j} w_{ij}^1{・}x_{ij} \qquad(2) \\\\
y^2&=&wsm({w^2},x)=\displaystyle \sum_{i,j} w_{ij}^2{・}x_{ij} \qquad(3)
\end{eqnarray}
$$
下図では畳み込み層の3つのニューロンによって、数万枚の手書き文字の数字を学習した3つの異なる局所的パターンと、その出力結果を表しています。
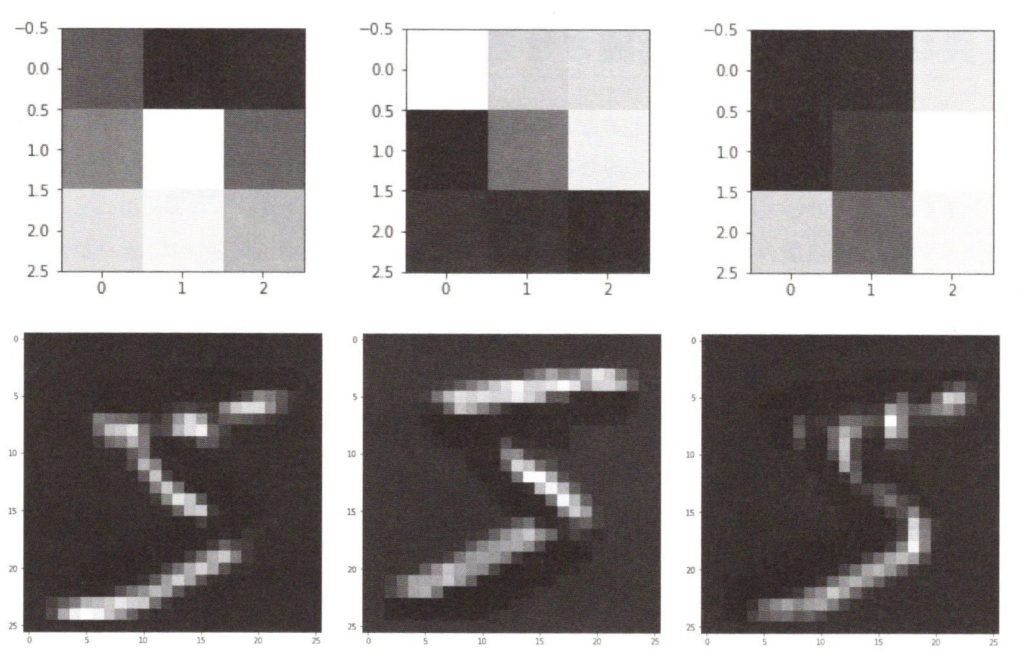
畳み込み層の局所的なパターンとその出力
上図は、3つのニューロンの畳み込み層を使う際に注意すべきは、出力が3つの値によって構成されていることです。これらの値については、出力画のそれぞれのニューロンごとに4✕4の2次元データとして保存され、3つのニューロンからの出力を纏めることで、4✕4✕3の3次元(3D)の出力データとなります。幅と長さは1個のニューロンの出力と同じで、畳み込みニューロンの数だけ深さが加わります。