猫や犬、自動車などの実世界のオブジェクトを含むような入力画像を認識するニューラルネットワークを作るには多くの畳み込み層を追加する必要があります。これを深層畳み込みニューラルネットワークと呼びます。
三次元データを受け付けられるようにする
深層畳み込みニューラルネットワークこそが、まさにディープラーニング、深層学習のモデルを構築しています。しかしながら、深層学習では、これまで説明してきた畳み込みニューロンの特徴の他にも、非常に重要な特徴があることを説明する必要があります。それは、最初の畳み込み層の出力は1個のニューロンの出力の2次元データ1枚1枚を重ねた3次元(3D)の構造になっていることです。畳み込み層を追加したいのなら、3次元データを受け付けられる様にしなければなりません。
2次元の入力データなら、畳み込みニューロンは受容野に入力データ\(F✕F\)の各値を対応付けるだけで良かったのですが、3次元データの場合は、深さ方向に拡張する必要があります。このとき、ニューロンの受容野は、入力データの枚数を深さ\(D\)とすると、\(F✕F✕D\)となります。
下図は畳み込みニューロンに対する2Dと3Dの入力データのイメージ比較を示しています。
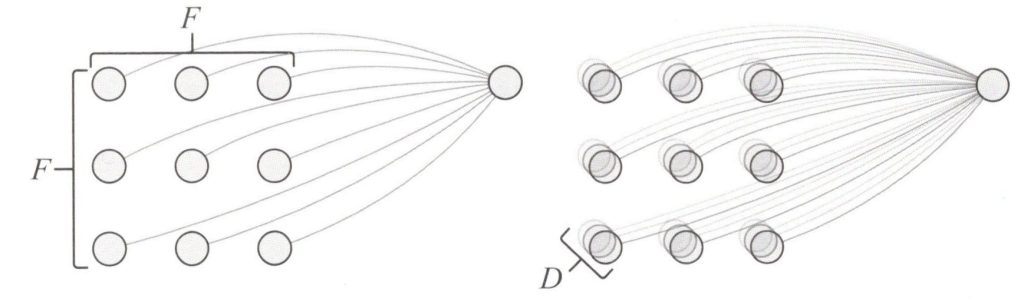
畳み込みニューロンに対する2Dの入力と3Dの入力
この畳み込みニューロンの演算は、2次元データの場合を拡張した次式で表せます。
\(\begin{eqnarray}
y=wsm(w,x)=\displaystyle \sum_{i,j,k} w_{ijk}・x_{ijk} \tag{1}
\end{eqnarray}
\)
ここで\(i\)と\(j\)は、ニューロンの受容野\(x\)と重み\(w\)が対応する3次元の入力データのは場と長さのインデックスで、\(k\)は深さのインデックスです。
これまでと同様に、このニューロンは入力データに対して、機械的にフォーカスを左から右、上から下にスライドさせますが、ある部分にフォーカスしているときに深さ方向にも対応し、\(F\)と\(D\)がいずれも3とすると、3✕3✕3で9個の入力値を\(wsm\)で同時に学習し、1個の出力値を生成することになります。
すべての畳み込み処理が終了すると、このニューロンは下図に示すような四角い形状の出力値を生成します。この四角い形は、2次元の場合と同じで、\(W\)を入力値の幅と長さ、\(F\)をニューロンの受容野の幅と長さとしたとき、\(W-F+1\)となります。
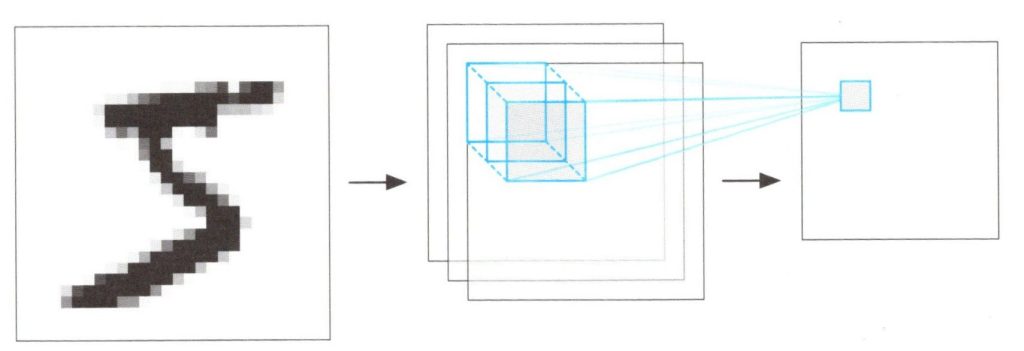
3次元の入力データに対する1個のの畳み込みニューロンの出力
シンプルなCNNモデルで2層目の畳み込み層を構築しようとすると、その前の階層に合わせて畳み込みニューロンを組み合わせる必要があります。2個のニューロンで畳み込み層を作ろうとした場合、この階層の出力データの深さは2になります、これはニューロンの数と同じというわけです。この畳み込み層は、4✕4✕3の形状の入力データに対して、2✕2✕2の形状の出力データを生成することになります。
下図は、この階層の畳み込み処理の様子です。
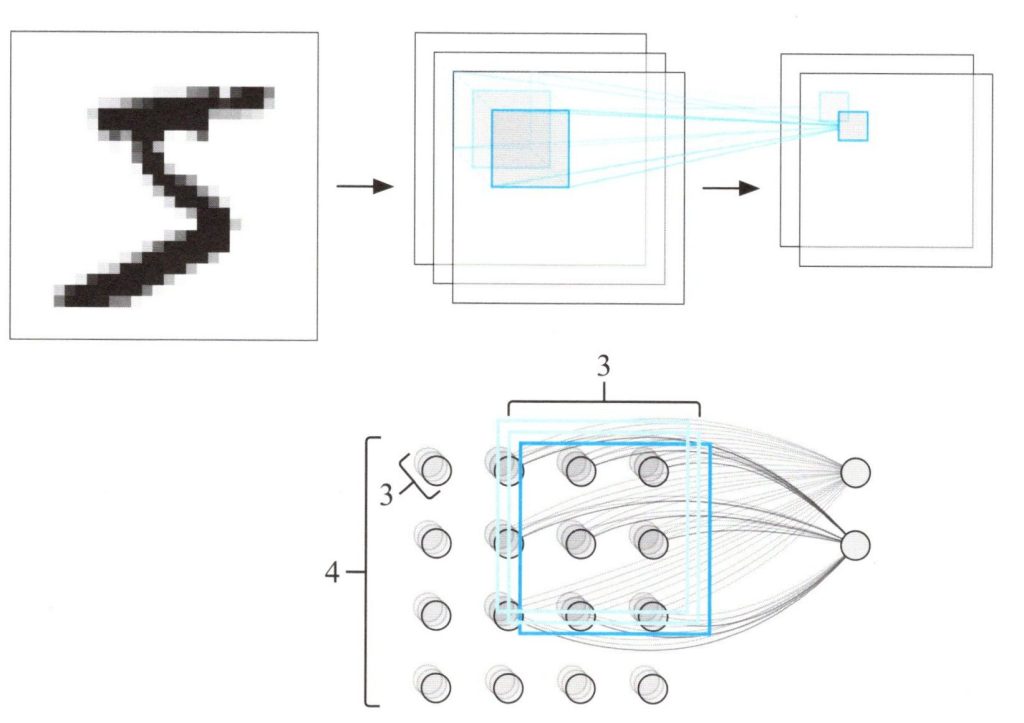
3次元の入力データに対する畳み込み層の畳み込み処理
また、深層畳み込みニューラルネットワークの特徴として、1層目のニューロンが、入力画像から意味のある局所パターンを認識して要約することで、2層目のニューロンに向けて、より使いやすい情報の形で受け渡す、ということが挙げられます。