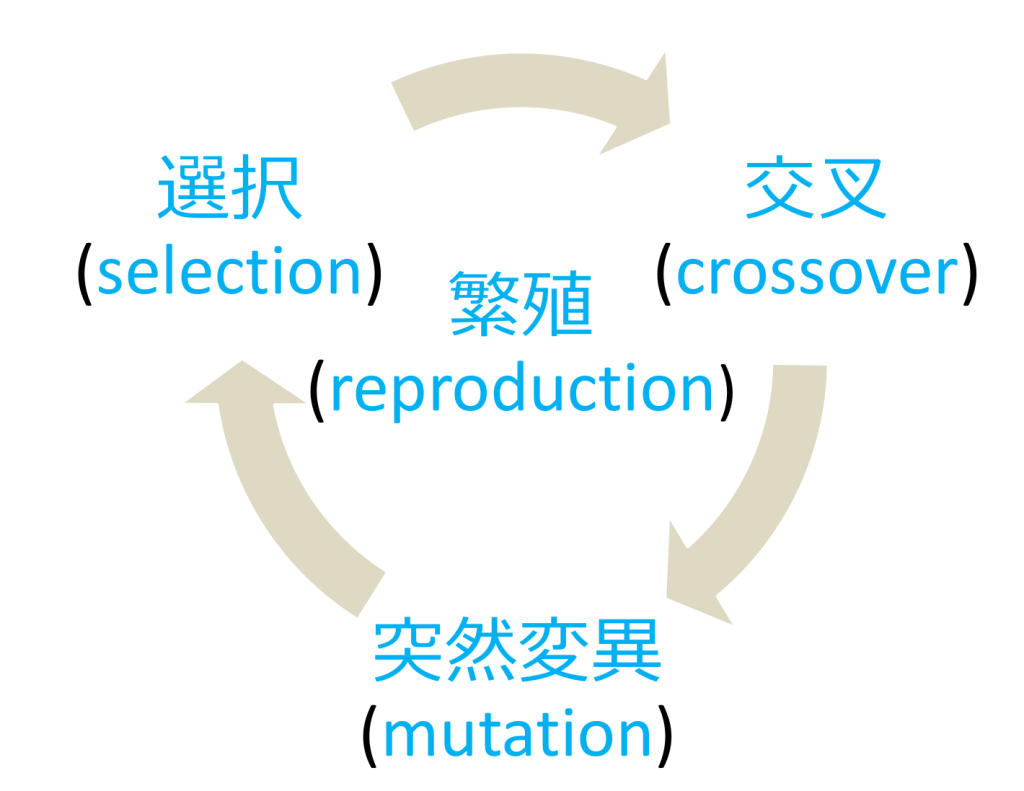
本記事では、遺伝的アルゴリズムの繁殖モデルの「選択」、「交叉」、「突然変異」についての基本的手法を簡潔にまとめています。
遺伝的操作(Genetic Operations)
遺伝的アルゴリズムの基本的イメージを図にすると、下図のようになります。
選択(selection)
適応度に基づいて、個体を増やしたり減らしたりする対象を選び出す操作です。これは生物の自然淘汰をモデル化したものです。選択の方式は主に次の4つに分けられます。
<ルーレット方式>
集団をルーレット版に見立て、ランダムな選択を行う方式です。各個体の適応度がルーレット版の面積と比例しており、適応度が高い染色体ほど選ばれる確率が高くなります。なお、ルーレット方式では適応度が正であることが前提となります。個体間の適応度の差が大きい場合、適応度の高い個体の選ばれる確率が高くなりすぎ、局所的な最適解への初期収束の原因となる点に注意が必要です。
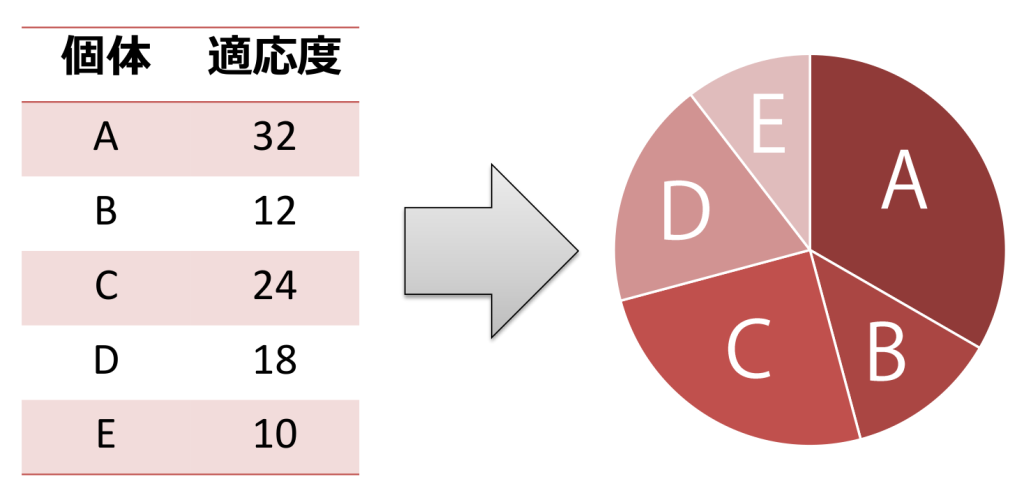
ルーレット方式を式で表すと下記のようになります。
$$
\begin{eqnarray}
p_i= \frac{f(i)}{\displaystyle \sum_{n=1}^Nf(n)}
\end{eqnarray}
$$
ここで、\(p_i\) : =ある個体が選択される確率、\(f(i)\) : 個体の適応度、N : =集団サイズ と定義しています。
<ランキング方式>
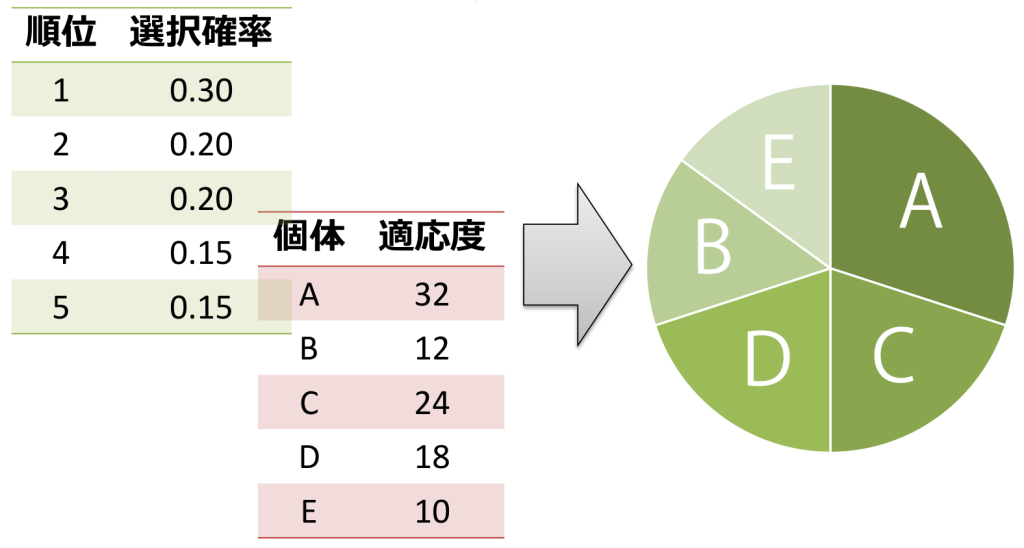
ランキング方式は、ルーレット方式を変形した方式です。適応度によって各個体のランク付けを行い、「1位なら確率\(p_1\)、2位なら\(p_2\)、・・・」と事前に決められた確率を適用する方式です。この方式は、個体間の適応度の差が選択確率に影響しませんが、適応度に差がない個体出会っても選択確率に大きな差が生じる可能性があります。そのため、ランク付けを行うためには世代毎にソートを行うことが必要です。
<トーナメント方式>
トーナメント方式は、予め決めた個体数(トーナメントサイズ)をランダムに抽出し、その中で最も適応度の高い個体を選択する方式です。トーナメントサイズを変更することで、選択圧をコントロールすることが可能になります。トーナメントサイズを大きくすることで選択圧を高めることが出来ますが、初期収束の原因となるので考慮が必要となります。
<エリート主義>
エリート主義は、予め決めた個数の、最も適応度の高い個体をそのまま次世代にコピーする方式のことです。世代間で適応度の最大値が下がらないことが保証される、という特徴があります。しかし、エリートの遺伝子が集団の中で広まりすぎて、解の多様性が失われる側面もあることを考慮に入れる必要があります。
交叉(crossover)
選ばれた2つの個体の遺伝子の一部を入れ替える操作を「交叉」と呼びます。これは生物の交配をモデル化したものです。
<交叉確率\(p_c\)>
各々の染色体において、交叉が発生する確率のことです。通常、80%〜95%として設定します。
基本的な交叉方式として以下の4つが挙げられます。
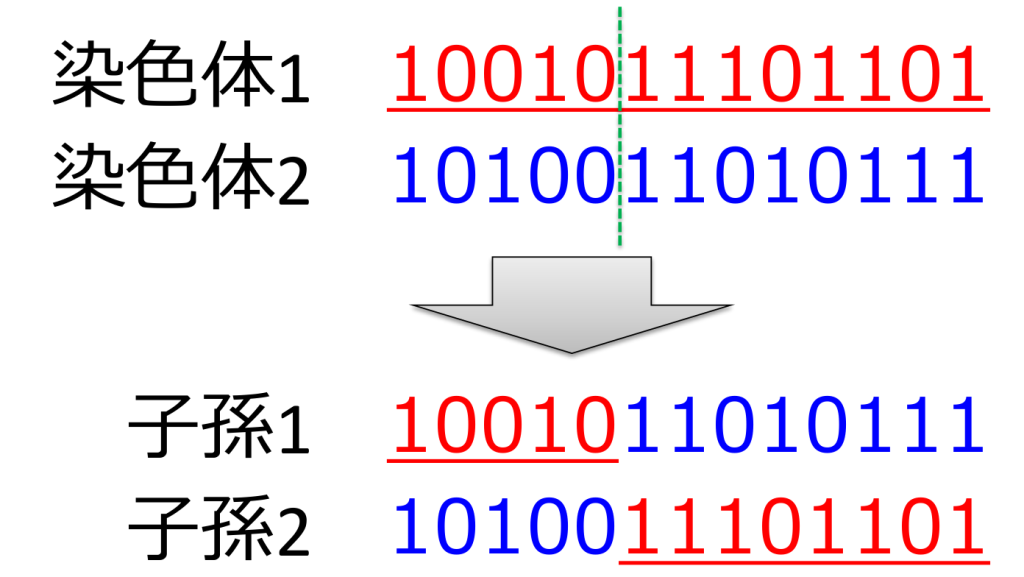
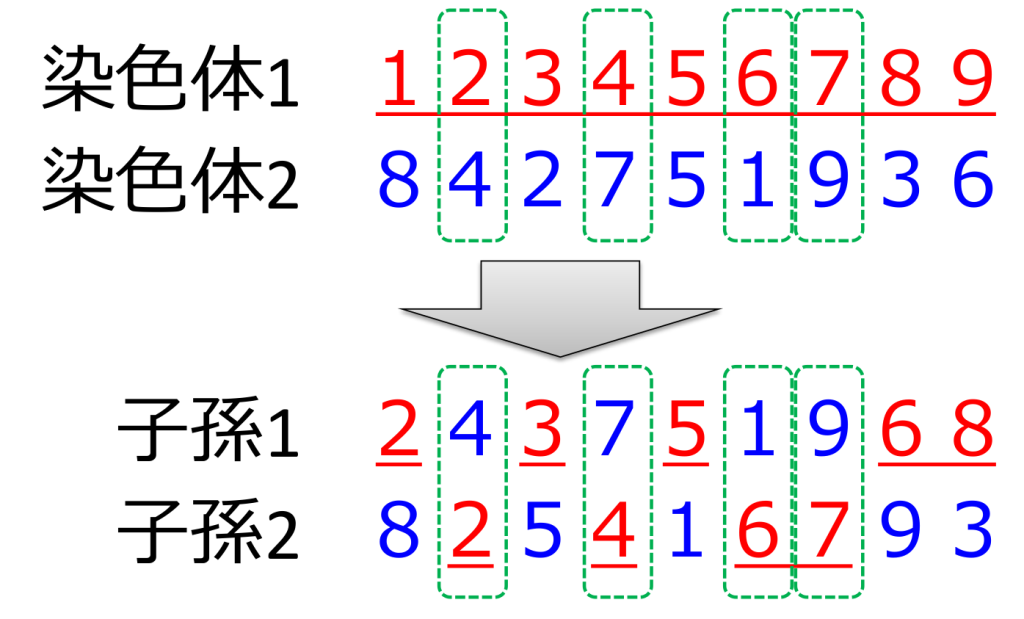
<一点交叉>
遺伝子が交差する場所(交叉点)をランダムに決定し、その場所より後ろの遺伝子を入れ替える方式。効率が低いため、現在はあまり用いられていません。親の遺伝子と子孫の遺伝子は、下記のようなイメージで交叉します。
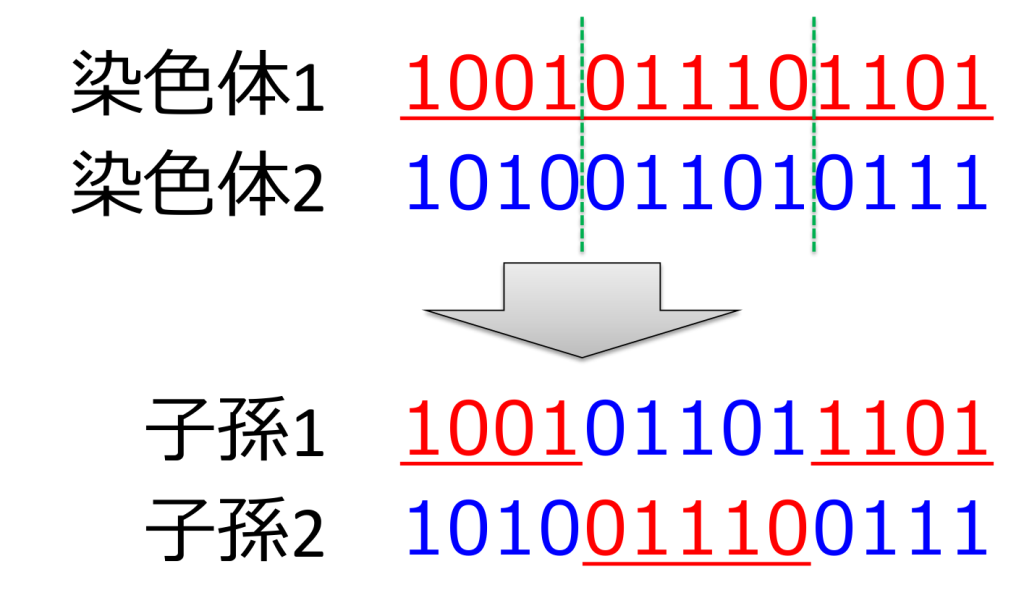
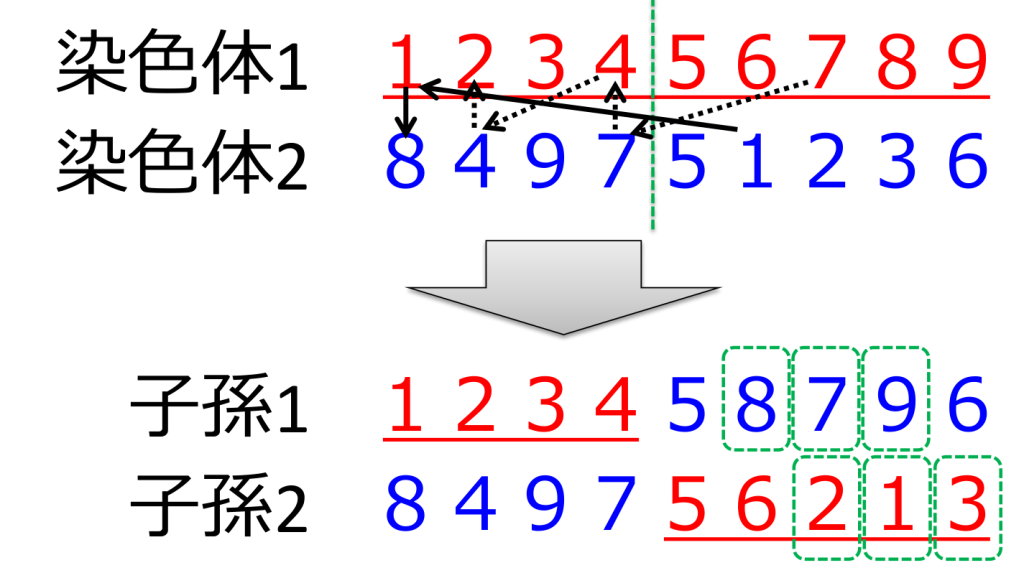
<二点交叉>
2つの交叉点をランダムに決定し、その間の遺伝子を入れ替える方式です。交叉イメージは下図のようになります。
<多点交叉>
3つ以上の交叉点を持つ方式です。二点交叉や一様交叉よりも良い値が得られることが殆どないため、あまり用いられていません。
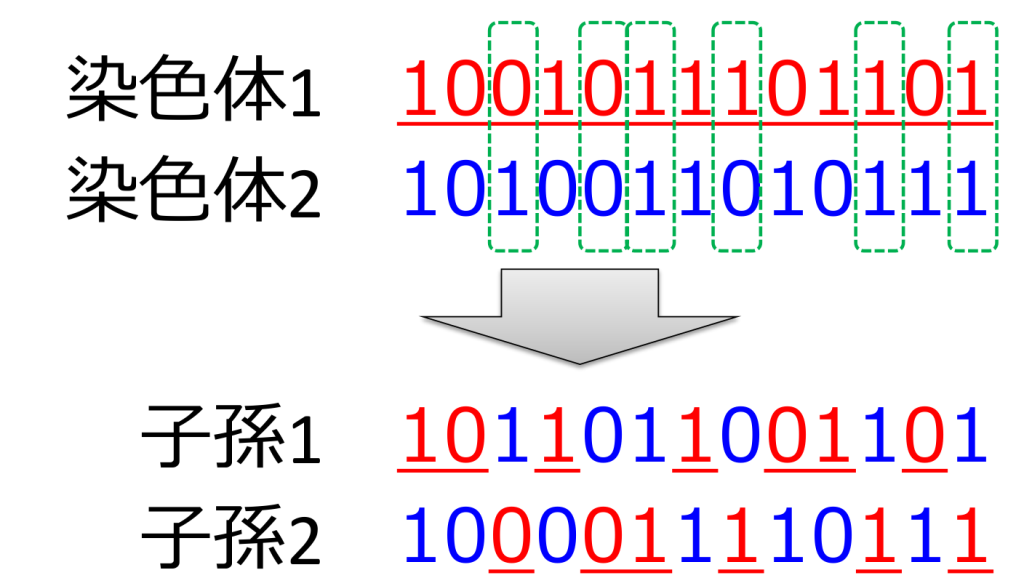
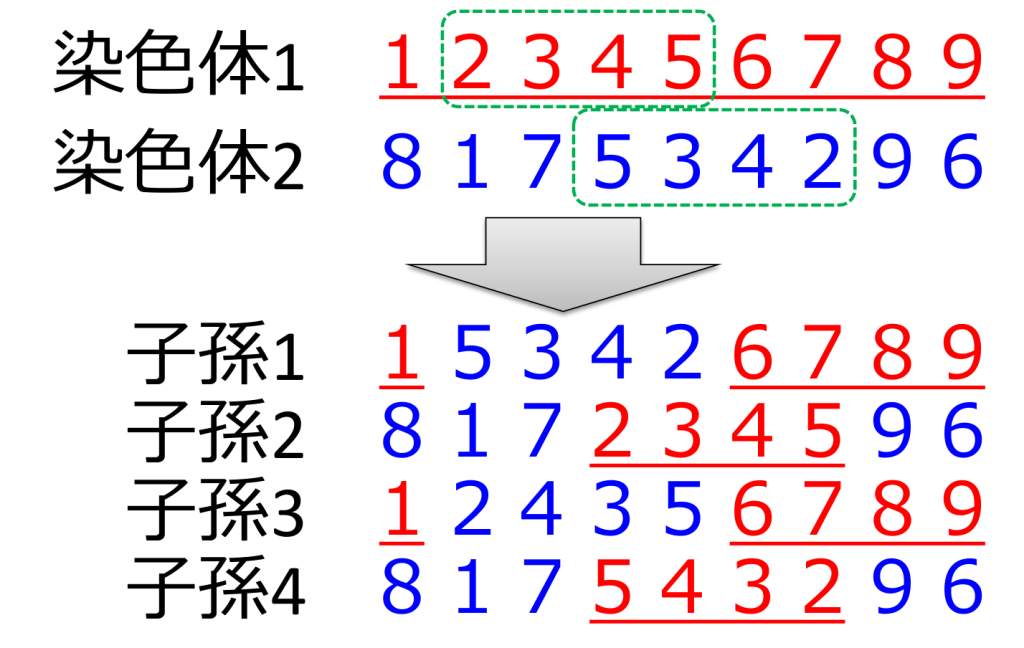
<一様交叉>
各遺伝子のそれぞれを所定の確率(通常は1/2)で入れ替える方式です。交叉のイメージは下図のようになります。
一様交叉は、二点交叉が得意とする問題を苦手とし、逆の性質を示します。ヒッチハイキング問題の対策として用いられます。
順列エンコーディングに対応した交叉方式
順列の交叉の特徴は「同じ遺伝子が重複しないこと」です。順列の交叉には次の8つの方式があります。
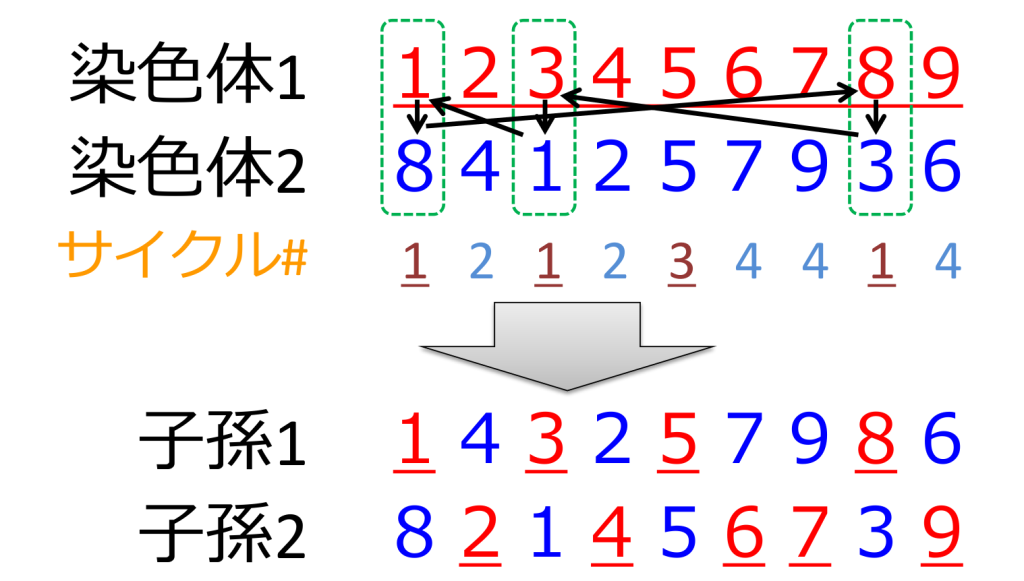
<循環交叉>(cycle crossover; CX)
双方の親から重複しない組み合わせを選んで、遺伝子の一部ずつを受け継ぐ方式です。
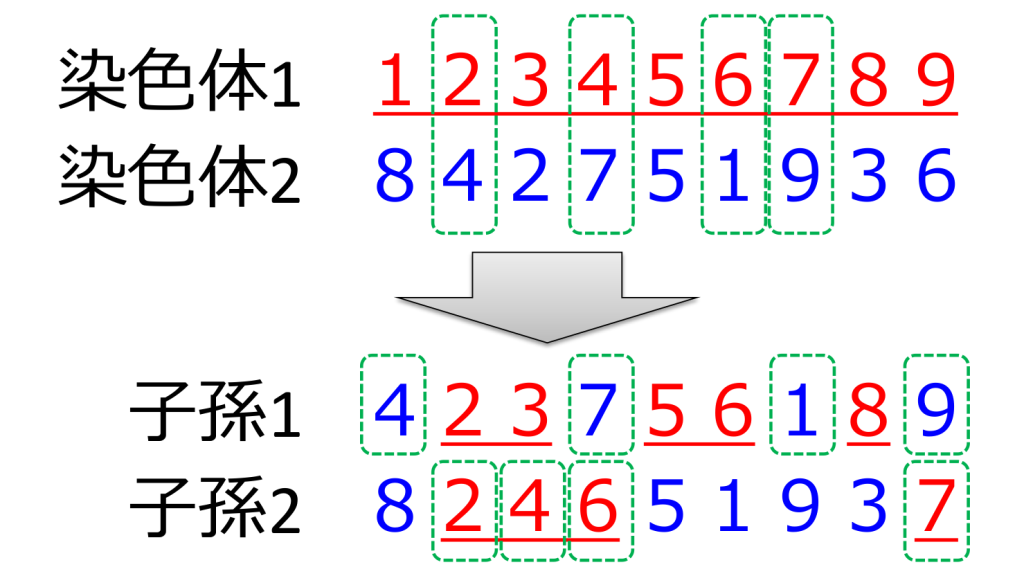
<順序交叉>(order crossover;OX)
片方の親からは一部をそのまま受け継ぎ、残りの部分についてはもう片方の親から相対的な順序を受け継ぐ方式です。

<一様順序交叉>(order-based crossover;OX2))
一様に選んだ遺伝子座について、一方の親の遺伝子の出現順序に従って、他方の親の遺伝子を並び替えたものを受け継ぐ方式です。
<一様位置交叉>(position-based crossover;POX)
一様に選んだ遺伝子を入れ替え、残りの遺伝子については親と同じ相対順序となるように配置する方式です。
<部分写像交叉>(partially mapped crossover;PMX)
片方の親\(P_1\)からは一部をそのまま受け継ぎ、残りの部分についてはもう片方の親\(P_2\)から重複しない遺伝子をヲのまま受け継ぐ方式です。重複する遺伝子については、\(P_1\)上で該当する遺伝子が占める遺伝子座を求め、\(P_2\)上の同じ遺伝子座に存在する遺伝子を受け継ぎます。
<サブツアー交叉>(subtour exchange crossover;SXX)
それぞれの親の間で、ある共通する数字の組み合わせからなる部分順列が存在する場合に、それを交換します。さらに入れ替えた部分順列を逆にしたものを含め、合計4個の子を生成します。
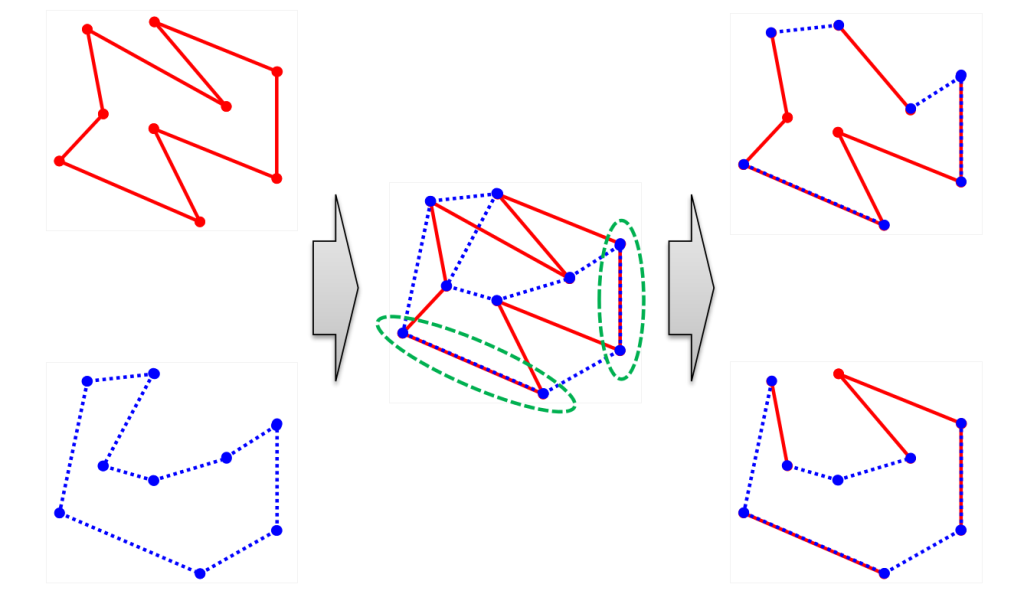
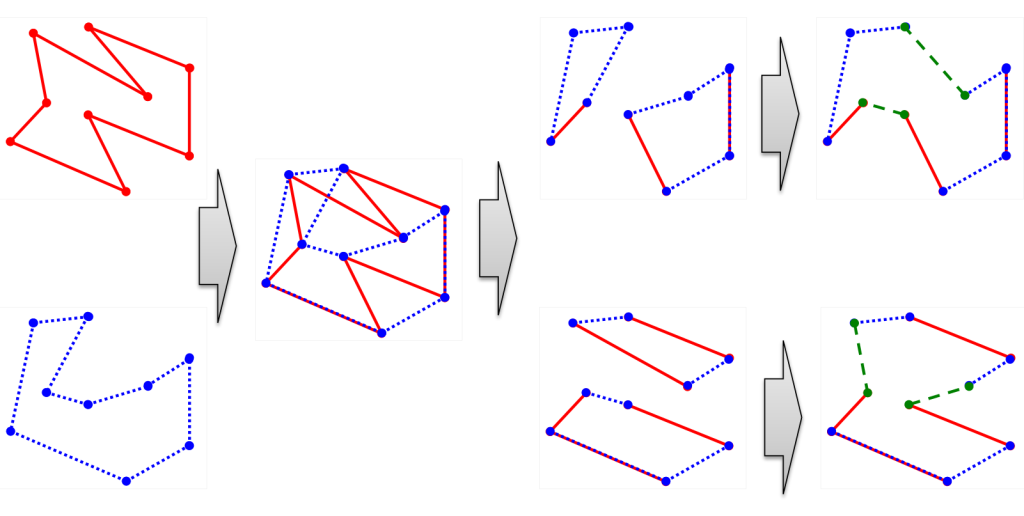
<辺組換え交叉>(edge recombination crossover;ERX)
順列の繋がり(辺)に着目した交叉方法です。双方の親が共通して保有する辺をなるべく受け継ぐように子を生成します。
<枝組み立て交叉>(edge assembly crossover;EAX)
両親のいずれかが保有する辺のみを用いて複数のサブツアーに分割された不完全解を生成します。サブツアー間をなるべく短い辺を用いて接続しなおすことで完全解を含む子を生成します。
経路問題への適用として、計算コストと精度の両面から、現時点において最も優れた方法とされています。
その他の交叉方式として、算術交叉(arithmetic crossover)や平均化交叉、ブレンド交叉(BLX-α)、単峰性正規分布交叉(UNDX)、シンプレックス交叉(SPX)などの方式があります。
突然変異(mutation)
個体の遺伝子の一部をランダムに変化させることを突然変異といいます。これも生物における突然変異をモデル化したものです。突然変異を加えることで、局所解に陥ることを防ぐ効果があります。
変異確率(\(P_m/))
各々の染色体において、突然変異が発生する確率のことです。通常0.1%〜1%、高くても数%として設定します。確率が低すぎると局所解に陥りやすくなり、高すぎるとランダム段作に近づいて解が収束しにくくなります。突然変異の基本的な方式は、以下の9つがあります。
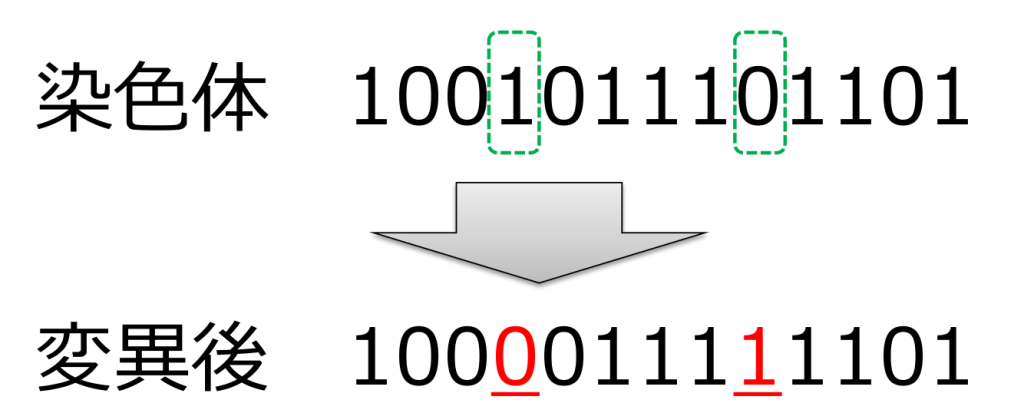
<置換(substitution)>
ランダムに選ばれた遺伝子を対立遺伝子に置き換える方式です。
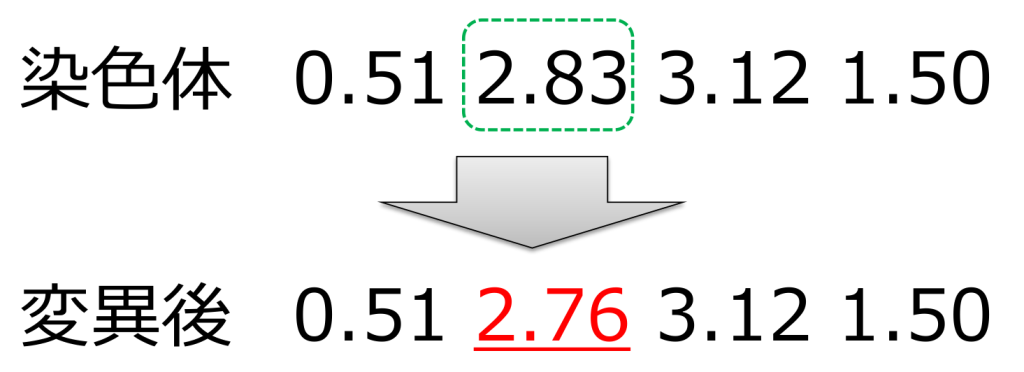
<摂動(perturbation)>
ランダムに選ばれた遺伝子の値に微量値を加算(または減算)する方式です。
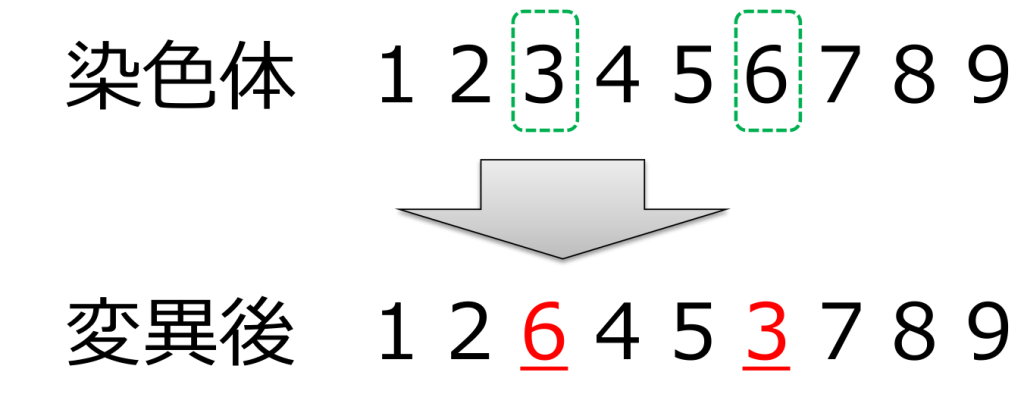
<交換(swap)>
ランダムに選ばれた2つの遺伝子を入れ替える方式です。
<逆位(inversion)>
ランダムに選ばれた2点間の遺伝子を逆順に並び替える方式です。
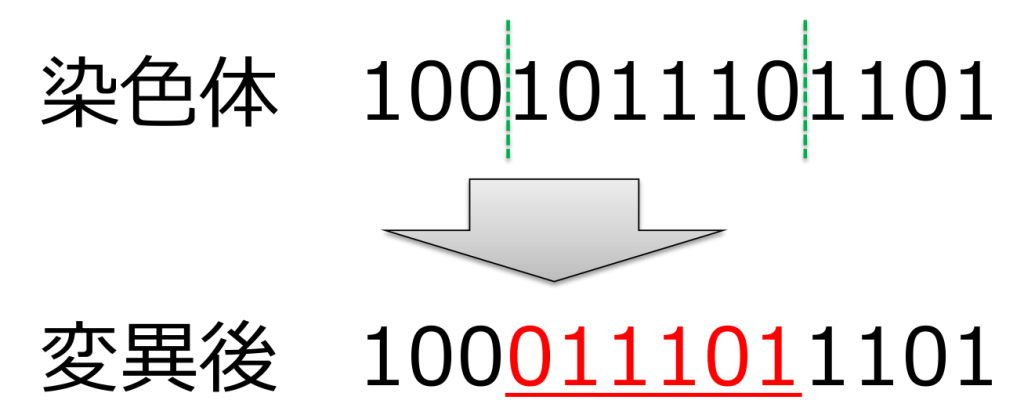
<撹拌(scramble)>
ランダムに選ばれた2点間の遺伝子をランダムに並び替える方式です。
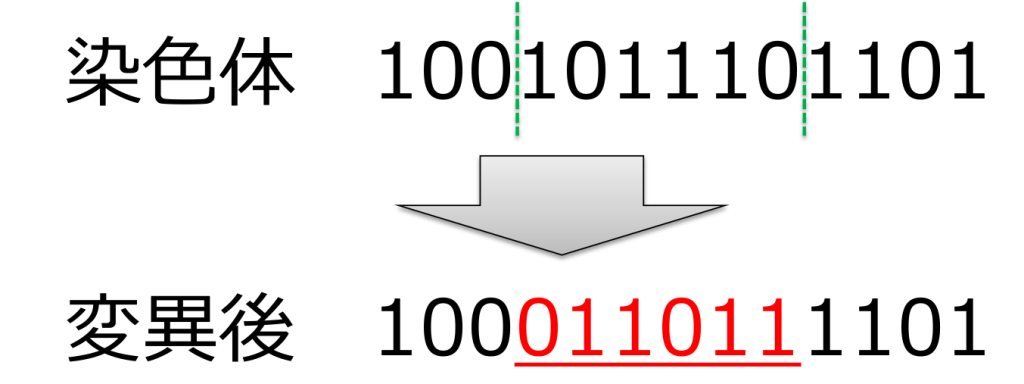
<転座(translocation)>
ランダムに選ばれた2点間の遺伝子を別の遺伝子座に移動する方式です。
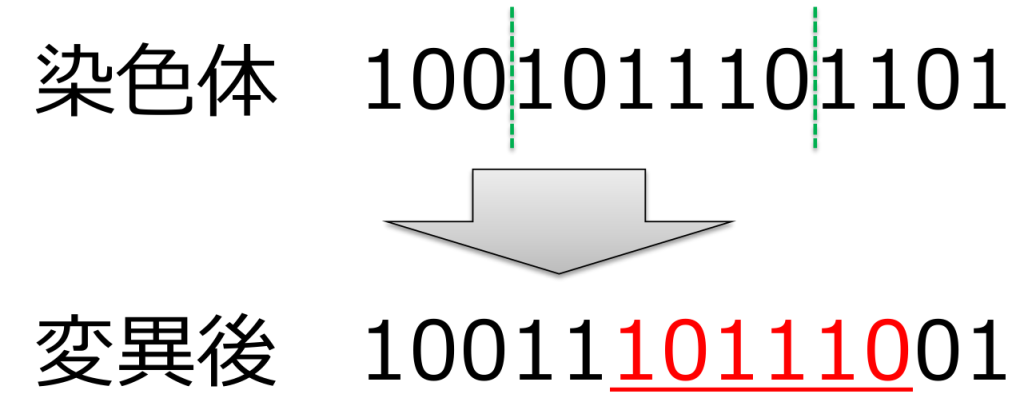
<重複(duplication)>
ランダムに選ばれた2点間の遺伝子を別の遺伝子座に複製する方式です。
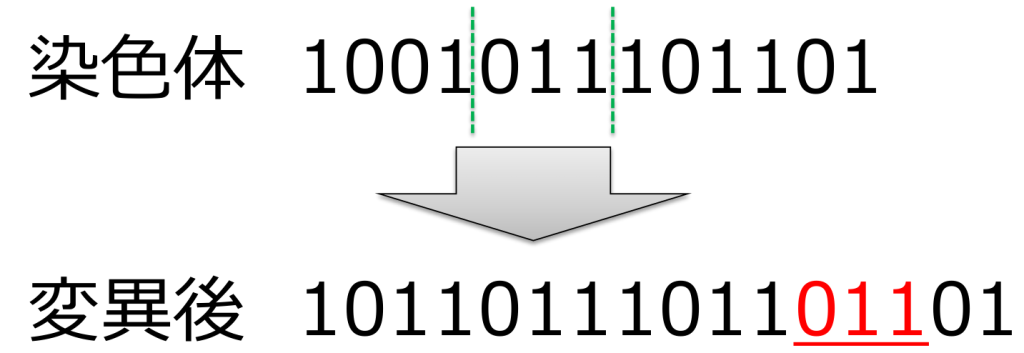
遺伝子長が変化
<挿入(insertion)>
ランダムに選ばれた場所に任意の遺伝子を挿入する方式です。
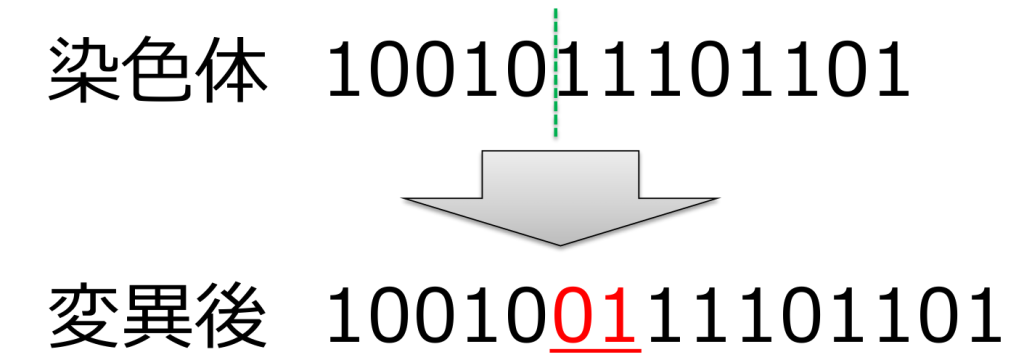
遺伝子長が変化
<欠矢(deletion)>
ランダムに選ばれた遺伝子を削除する方式です。
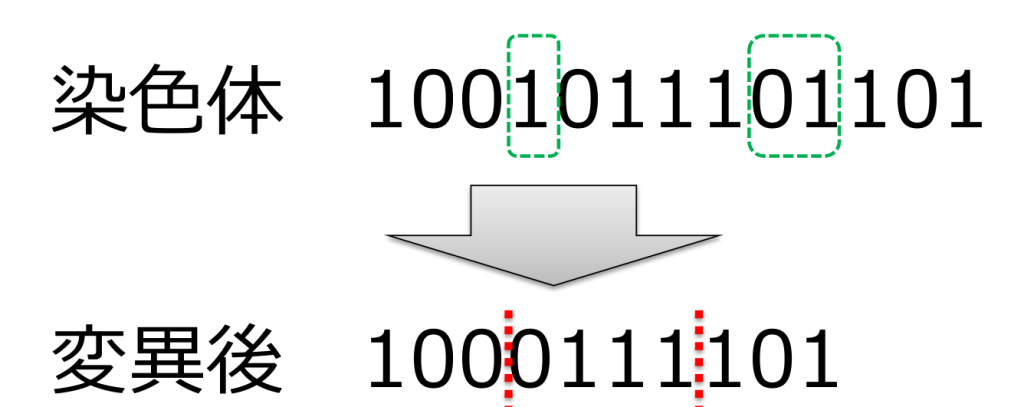
遺伝子長が変化