前の章では、多層パーセプトロン=ニューラルネットワークがどの様な背景で生まれ、どんな問題に対して、どの程度の学習能力があるかについて説明しました。線形な問題でも、非線形な問題でもニューラルネットワークはうまく学習してくれます。では、ニューラルネットワークはどの様に学習するのでしょうか。この部分について本記事で触れます。
ニューラルネットワークの学習方法
実はニューラルネットワークを含む機械学習では、どのアルゴリズムを用いようが必ず学習データが必要です。機械学習のアルゴリズムは、学習させないとなんの役にも立たないので、必ずデータを用意して学習させる必要があるのです。
何かしらのデータを読み込んで、そのデータに対して学習を行うわけですが、機械学習アルゴリズムは、入力されたデータに対応する正解を教えてもらう必要があります。これを教師あり学習(Supervised Learning)と呼びます。誰か教師役の人が与えたデータに対する正解を示してあげると、機械学習アルゴリズムは学習できるというわけです。
一方で、データだけを与えて正解を示さなくても学習することが出来ます。これを教師なし学習(Unsupervised Learning)と呼びます。もしくは、直接的に正解を示さず、学習結果を用いてなにか別のタスクを与えた時、良い結果を得られたか否かを判断するやり方もあります。これを強化学習(Reinforcement Learning)と呼びます。やりたい課題によって、いろんな学習方法があるわけですね。
教師あり学習(Supervised Learning)
教師あり学習というのは言ってみれば教師がいて、正解なら○、不正解なら✕を確認しながら機械学習プログラムが学習していく学習方法のことです。先生の代わりに正解データを用意してある場合もあります。
ニューラルネットワークは、この教師あり学習によって、どんどんと学習していくことが出来ます。ニューラルネットワークの他にも、決定木、サポートベクターマシン、ベイジアンネットワーク、ブースティングなど、様々な機械学習が考案されており、様々な場面で活用されています。
教師なし学習(Unsupervised Learning)
教師なし学習というのは教師あり学習と違って、教師はいませんし、正解データもありません。学習対象のデータがポンと渡されるだけというわけです。このデータだけを使って学習するのが、教師なし学習と呼ばれるものです。
「そんなことが可能なのか?」と思うかもしれません。でもよくよく考えてみると、人類が生まれてきて、動物やモノに名前をつけたり、似たようなものを分類するしたりする時、少なくとも最初にやってみようと思った人にとっては先生もいませんし、正解もありませんよね。正解はわからないけれども、見た目や雰囲気で違いがわかるようになることが、教師なし学習というわけです。
ニューラルネットワークでは、学習データを入力データとし、同じデータを正解データとしたり、少し加工して正解データとしたりすることで、教師なし学習を実現します。具体的には、オートエンコーダなどが有名です。この他、教師なし学習をする機械学習アルゴリズムとして、クラスタリングや次元縮約と言われる分野のアルゴリズムはたくさん提案されています。
強化学習(Reinforcement Learning)
強化学習というのは教師なしでも教師ありでもない学習ですが、教師がいないというわけではなく、厳密には、教師が答えを教えずに、上手く出来たときにのみ褒める学習です。
もう少し具体的に見ると、ニューラルネットワークが入力データに対して出力した答えについて評価してみて、良い答えだったら報酬を与えます。ニューラルネットワークは、この報酬を最大化するように行動を修正(パラメータ調整)します。ニューラルネットワークによる強化学習としてはQ学習、Sarsa法、モンテカルロ法などが有名です。
ニューラルネットワーク以外の機械学習アルゴリズムにも強化学習は適用できます。強化学習は報酬を最大化するように学習する学習方法が適用できれば、どんなアルゴリズムにも適用可能です。
学習プロセスから見る損失関数
ニューラルネットワークの場合では、いずれの学習も可能なのですが、ここではニューラルネットワークの一番基本的な学習プログラムである教師あり学習について説明していきます。ニューラルネットワークの教師あり学習は、具体的には次のステップで学習を行います。
Step 1.学習対象のデータを用意する
Step 2.データを入力データ(課題)と出力データ(正解)に分ける
Step 3.ニューラルネットワークにデータを入力する
Step 4.ニューラルネットワークの判定結果と出力データを比較する
Step 5.判定結果と出力データの差分をフィードバックする
Step 6.ニューラルネットワークのパラメータを更新する(Step3へ戻る)
判定結果と出力データを比較して、ほとんど誤り(誤差)がなかったか、指定した回数や時間が経過した場合は、そこで学習は終了します。
ここで、誤り(誤差)がどの程度であったかが、学習の終了条件になっています。誤差を、学習の度合いを表すものと考えているわけです。誤差が少なくなればなるほど、そのニューラルネットワークはよく学習していて、賢いといえます。神経回路網モデルでは、デルタ則とよんでいたものに相当します。
ニューラルネットワークでの教師あり学習例
まず、1つの正解データと、誤っているデータの事例を集めます。次に、学習対象のデータを正例と負例のようにいくつかのカテゴリに分け、ニューラルネットワークに学習させます。この時ニューラルネットワークは、負例のデータから「これは誤りですね」と学習し、正例から「これは正解ですね」と学習できるわけです。
学習対象の課題データのうち、例えば誤った負例が正解になるデータをニューラルネットワークに入力すると、ニューラルネットワークは、最初のうちは正例と判定したり、負例と判定したりします。この時、判定結果と出力データ(正解)とを比較して、どの様に誤判定(誤り)があったかを計算します。
この誤り(誤差)について、機械学習アルゴリズムの世界では損失(loss)と呼んでいます。また、判定結果が正解か、誤っているのかを判定し、その誤差を評価する関数を損失関数(Loss Function)と呼びます。
ニューラルネットワークは、フィードバックされた損失の程度に従って、次回は正しく正解できるように(誤差が少なくなるように)パラメータを更新する、というわけです。つまり、これがニューラルネットワークが学習している部分になります。学習が十分でないと判定された場合は、上記のStep 3.へ戻り、引き続き学習します。
損失関数のいろいろ
一般的なデータは、数字のリストで表現できることが多いので、Pythonではリスト型で取り扱うことが多いでしょう。また、損失関数自体にもいろいろなものが考えられています。
よく使うものには二乗和誤差(Mean Squared Error)や交差エントロピー(Cross Entropy Error)などがあります。それぞれを数学的な記述方法で表した場合は以下のようになります。
<二乗和誤差>
\(\begin{eqnarray}
E = \displaystyle \frac{1}{2}\displaystyle \sum_{k}{(y_k-t_k)}^2 \tag{1}
\end{eqnarray}
\)
ここで、\(y\)は機械学習アルゴリズムが判定した結果の出力データ、\(t\)は正解データです。その差を取って、2乗したものをすべての出力データについて加算し、1/2をかけ合わせたものが二乗和平均誤差です。
ちなみに、定数部分の1/2の存在理由は、二乗和誤差の式を微分したときに出てくる「2」という定数を打ち消すために添えられているもので、これについてはあまり意識する必要はありません。
<交差エントロピー誤差>
\(\begin{eqnarray}
E = -\displaystyle \sum_{k}{(t_k)}\log_{ e }( y_k) \tag{2}
\end{eqnarray}
\)
次に、交差エントロピー誤差について説明します、交差エントロピーというのは、「あるグループAと、あるグループBがどれくらい異なるか」について表しているものです。ここでは出力データ\(y\)と、正解データ\(t\)がどれくらい異なるのかを評価します。二乗和誤差の場合と違って、\(y-t\)のように単純に計算が出来ない場合にも用いることが出来ます。例えば、正解が「犬」または「猫」だった時、\((y_犬-t_猫)\)は誤差0といえますが、\((y_犬-t_猫)\)や\((y_猫-t_犬)\)の誤差って???となりますよね。
そのため、\(t_0=犬\)、\(t_1=猫\)、である正解データ\(t\)を、one-hotと呼ばれる形式\(t_0\)={1,0}、\(t_1\)={0,1}としておいて、出力データ\(y\)と比較できる形にします。出力データは、例えば犬と猫のそれぞれを持つ確率で、\(y_0\)={0.67,0.33}、\(y_1\)={0.12,0.88}のように表現します。
これらによって、交差エントロピー誤差は、出力データに含まれる、各ラベルの確率のうち、正解が得られる確率を抜き出すことが出来るので、この確率を対数化(Logをとる)したものを合計すれば良いわけです。具体的には、\(t_0\)={1,0}の正解データに対して、\(y_0\)={0.67,0.33}が与えられた時、交差エントロピー誤差は次のように計算できます。
\(\)
\begin{eqnarray}
E_0 &= &-\displaystyle \sum_{k}{(t_{0,k})}\log_{ e }( y_{0,k} ) \\
&=& -t_{0,0}\log_{e}(y_{0,0}) -t_{0,1}\log_{e}(y_{0,1}) \\
&=&-1.0\log_{e}(0.67) -t_{0,1}\log_{e}(0.33) \\
&= & 0.400 \\ \tag{3}
\end{eqnarray}
\(\)
\(t_1\)={0,1}の正解データに対して、\(y_1\)={0.12,0.88}が与えられらときは次のようになります。
\(\)
\begin{eqnarray}
E_0 &= &-\displaystyle \sum_{k}{(t_{1,k})}\log_{ e }( y_{1,k} ) \\
&=& -t_{1,0}\log_{e}(y_{1,0}) -t_{1,1}\log_{e}(y_{1,1}) \\
&=&-1.0\log_{e}(0.12) -t_{0,1}\log_{e}(0.99) \\
&= & 0.128 \\ \tag{4}
\end{eqnarray}
\(\)
正解が犬{1,0}であった\(t_0\)に対しての判定結果\(y_0\)の交差エントロピー誤差\(E_0\)は0.400、正解が猫{0,1}であった\(t_1\)に対しての判定結果\(y_1\)の交差エントロピー誤差\(E_1\)は0.128でした。この結果から、どちらかというと\(t_0\)の犬データに対しての誤差の方が大きいことから、よりパラメータ調整が必要なことがわかります。
ちなみに、交差エントロピーの「交差」とは犬猫の例では、犬と猫、猫と犬を違い比較することを意味しており、エントロピーというのは、ある確率\(P\)で発生する事象の情報量のことです。エントロピーは\(-Plog(P)\)で表しますが交差エントロピー誤差では、\(-log(P)\)のみ扱います。特徴としては、下図のように確率\(P\)が0~1の範囲をとるため\(-log(P)\)は\(∞\)〜0のなだらかな単調現象の式になります。
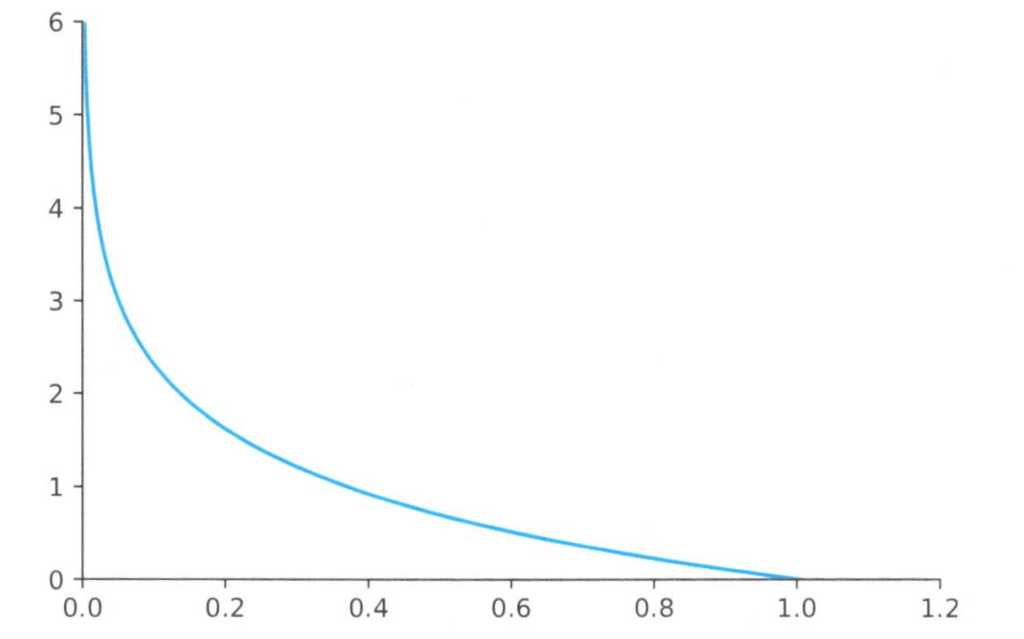
\(-log(P)\)のグラフ
完全に正解tと一致する出力yが得られた場合は、誤差は0になります。