ディープラーニングといえば、ニューラルネットワークです。ニューラルネットワークは
脳の振る舞いを模倣した神経回路網を数式で表したネットワークモデルです。
この章では、ニューラルネットワークの基本的な考え方としてパーセプトロンを紹介します。
パーセプトロンとは、脳の神経細胞を単純化したニューロンを用いたプログラムです。次に
ニューロンで利用されている活性関数を説明し、ニューロンを多段につなぎ合わせたニューラル
ナットワークについて説明します。
さらにニューラルネットウワークを利用して実際に正しく判定できるようになるための
損失関数の考え方、勾配法を用いた学習理論、最後に誤差逆伝搬法(バックプロパゲーション)
と呼ばれるニューラルネットワークの肝になるアルゴリズムについて詳細に説明します。
ニューロンとパーセプトロン
脳は膨大な数の神経細胞(ニューロン)から構成されており、このニューロンが脳の基本単位
です。ニューロンがお互いに結合することで巨大なネットワークを作り出し、学習機能や
情報処理の機能を実現しています。
近年急速に発達しているニューラルネットワークは人工ニューラルネットワーク(ANN:
Artificial Neural Network)と呼ばれています。
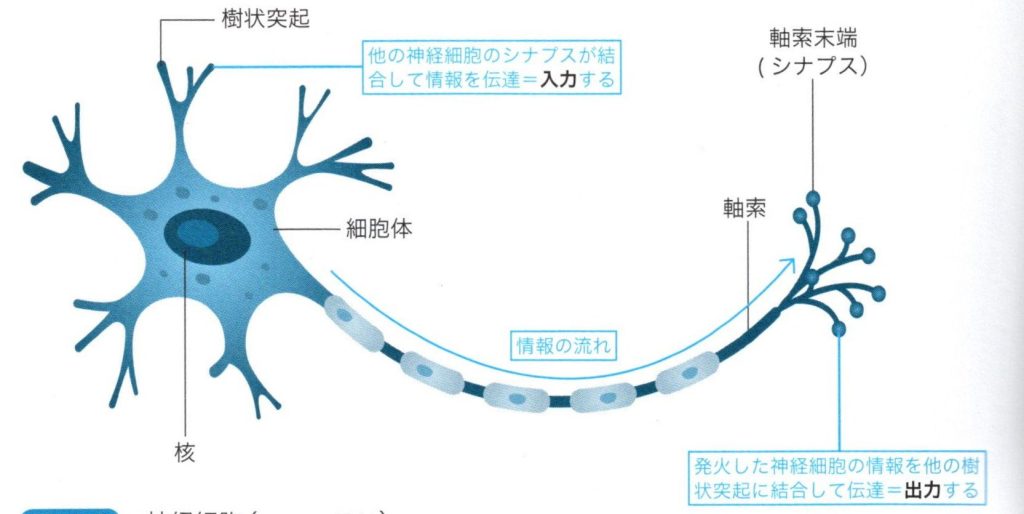
神経細胞(ニューロン)
上図のように、ニューロンは細胞体、樹状突起、軸索と呼ばれる部分からなります。
樹上突起は入力(インプット)、軸索は出力(アウトプット)と考えます。ニューロンは
樹状突起から入力された電気信号が神経細胞内の電位を超えるかどうかの閾値(Threshold:しきい値)
を持っていて、この閾値を超えるとニューロンは興奮した状態になり、軸索から電気信号が出力
されます。
このような、脳の基本単位であるニューロンをANNで表すと、次のような数式になります。
$$
\begin{eqnarray}
Z &=& f \left( {\mu} \right) \\
&=& f \left( \displaystyle \sum_{i,j}^{n} {w_{ij}} -h \right) \\ \tag{1}
\end{eqnarray}
$$
1つのニューロンは、n個のニューロンから入力\(x_i\)を受け取って、その入力値に係数\(w_i\)を掛けて
合計したものが閾値hを超えた場合に興奮(発火)したと考えます。このときANNの中でも最も単純なモデル
であるマカロック・ビッツの形式ニューロン(formal neuron)では、出力zはμが閾値hを超えたときに1、
そうでなければ0とし、以下のような図と数式で表せます。
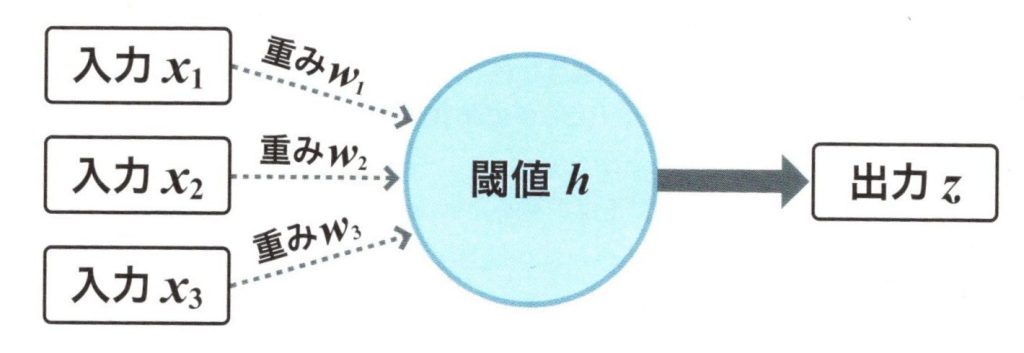
形式ニューロン
[ステップ関数]
\(\begin{eqnarray}
Z
=
\left\{
\begin{array}{l}
1 \qquad μ>hのとき \\
0 \qquad それ以外 \tag{2}
\end{array}
\right.
\end{eqnarray}
\)
グラフで表すと下図の様に階段状の関数となるため、階段関数またはステップ関数と呼びます。
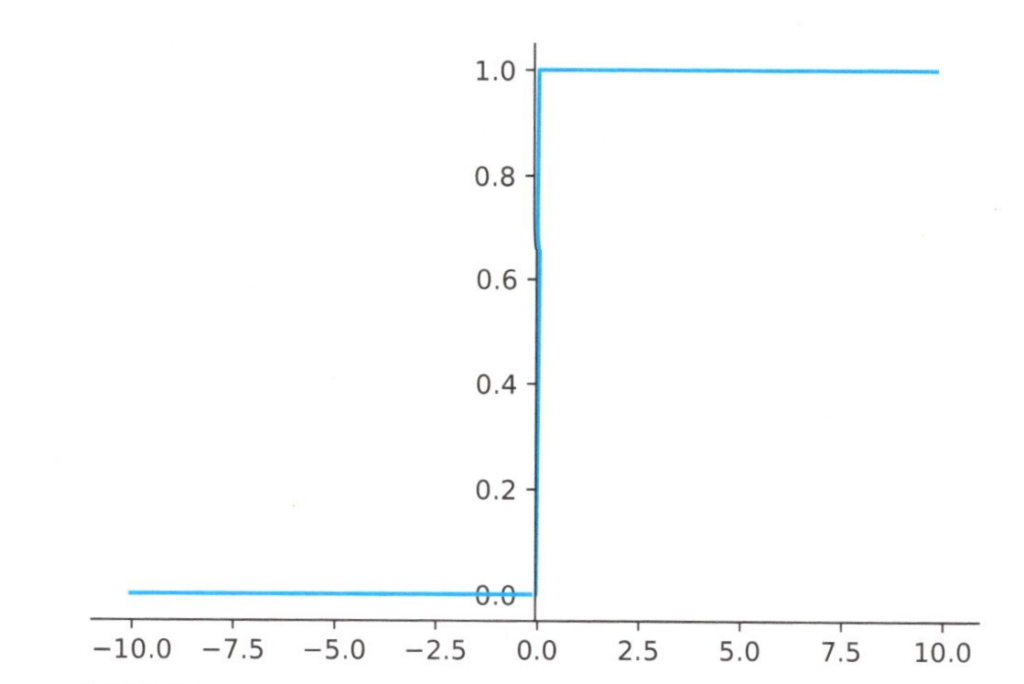
ステップ関数のグラフ
パーセプトロン
単一なニューロンは、これまでで触れたようなモデルで表すことが出来、係数\(w_i\)や閾値hを
調整することで学習することが出来ます。このような人工ニューラルネットワーク(ANN)の
モデルで学習する仕組みをパーセプトロンと呼んでいます。
上述の繰り返しとなりますが、パーセプトロンは神経細胞で構成される視覚や脳の機能を模して
数式でモデル化した人工的なニューロン(形式ニューロン)によって構成された人工ニューラルネット
ワーク(ANN)のことです。このモデルは統計の分野で用いられるロジスティックス回帰と呼ば
れる回帰分析の手法とも等価であることが知られています。
この様に、神経細胞をモデル化したものと、統計分野の回帰モデルが同じ数式で表現できること
は興味深く、さらにこの事実が、コンピュータによるシミュレーションや、学習の最適化を行う
際の理論構築の基礎になっていることが、現在の機械学習や統計学的なデータ分析の発展に
役立っていると言えるでしょう。
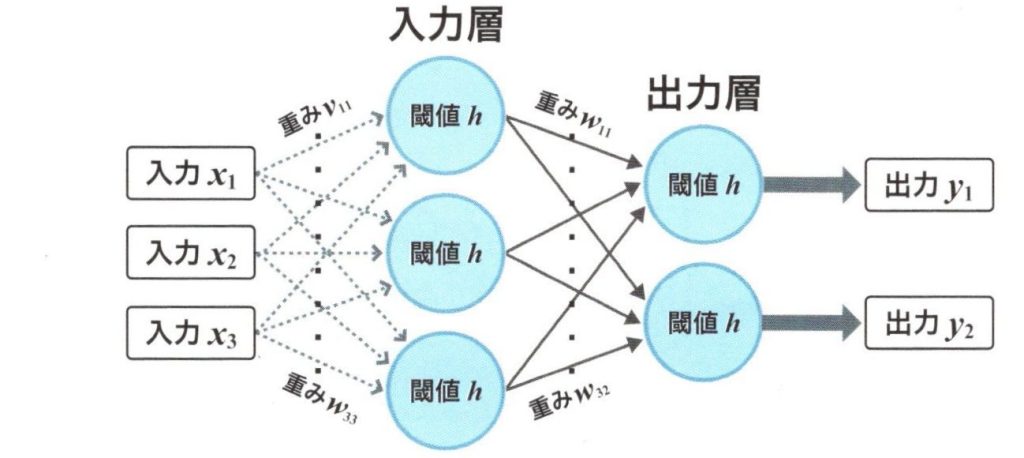
2層パーセプトロン