ここまでで、ニューラルネットワークの基本要素であるニューロンについて説明してきました。単一のニューロン(形式ニューロン)を利用することでもある程度の学習能力を持っています。具体的には、犬と猫を分離する、というようなケースで学習可能です。
犬と猫を分類する
犬と猫を、そのサイズと人への慣れ具合から考えます。下図のケースでは1匹の犬と1匹の猫を分離します。
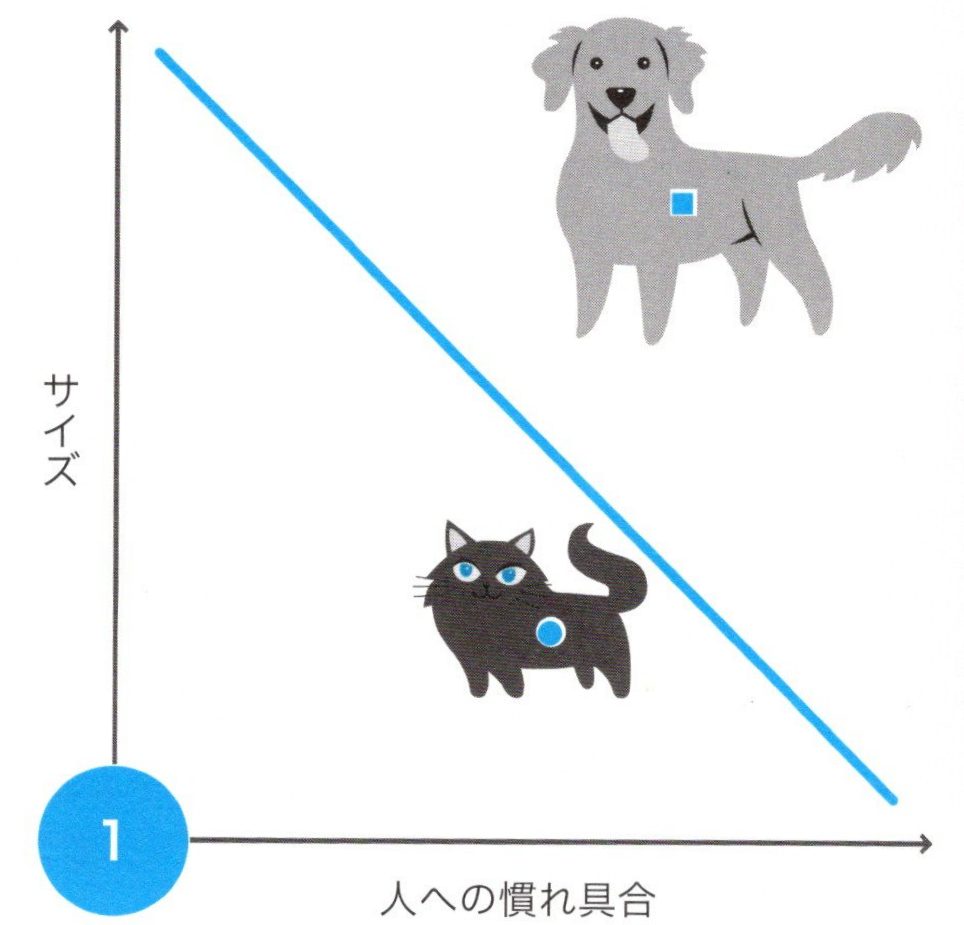
犬と猫の分離(1)
次に、さらに別の犬を下図で分類してみます。
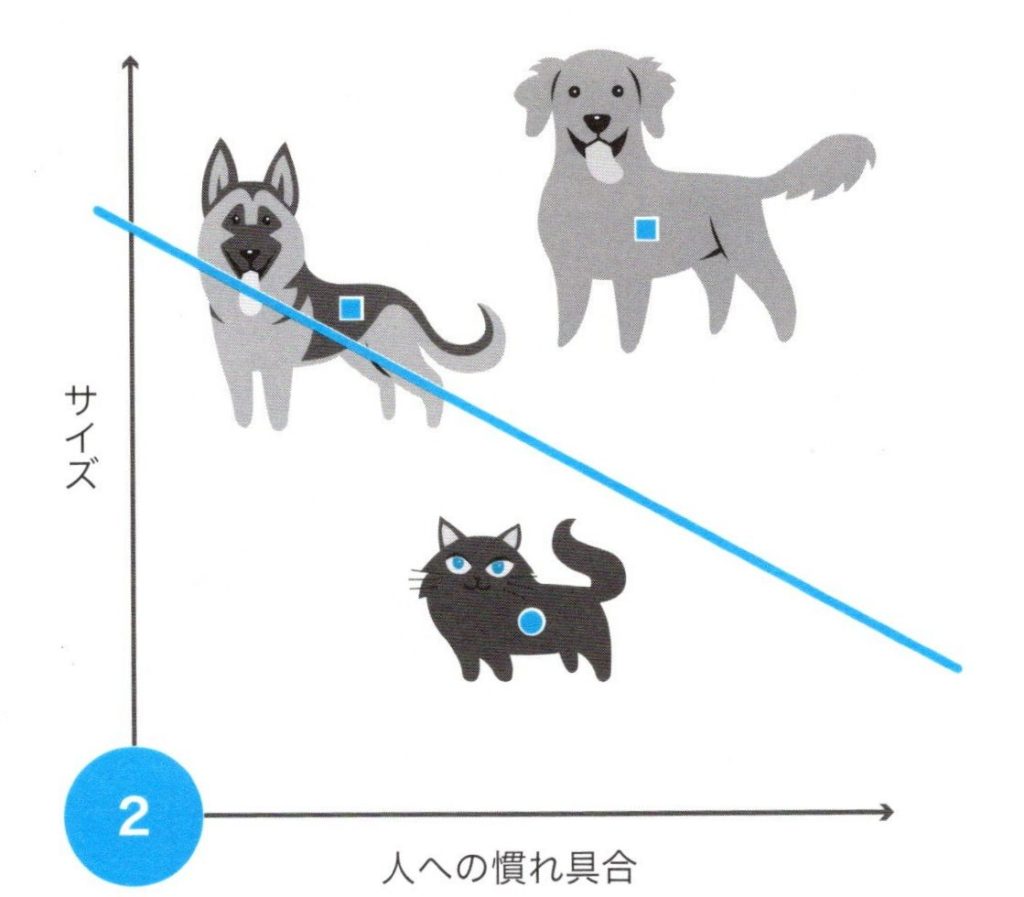
犬と猫の分離(2)
さらに下図では、1匹の犬と1匹の猫を追加します。
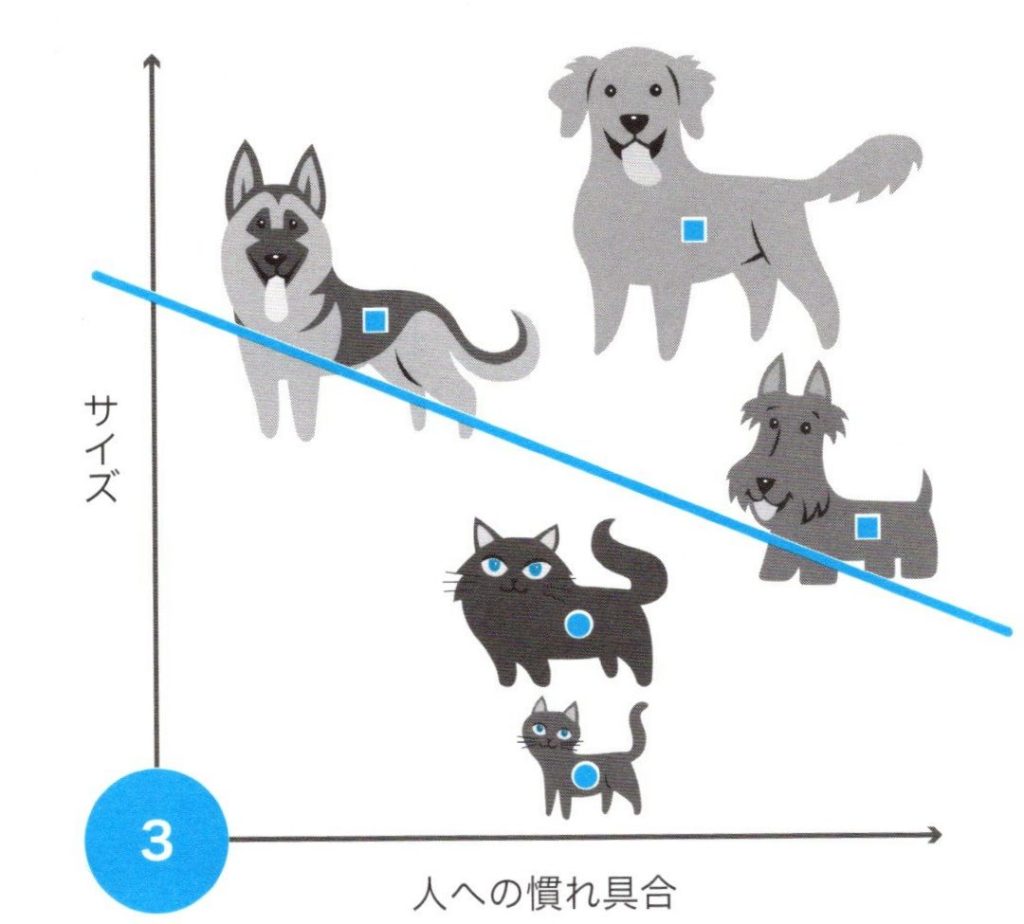
犬と猫の分離(3)
最後に下図では1番小さい犬のチワワを追加しました。
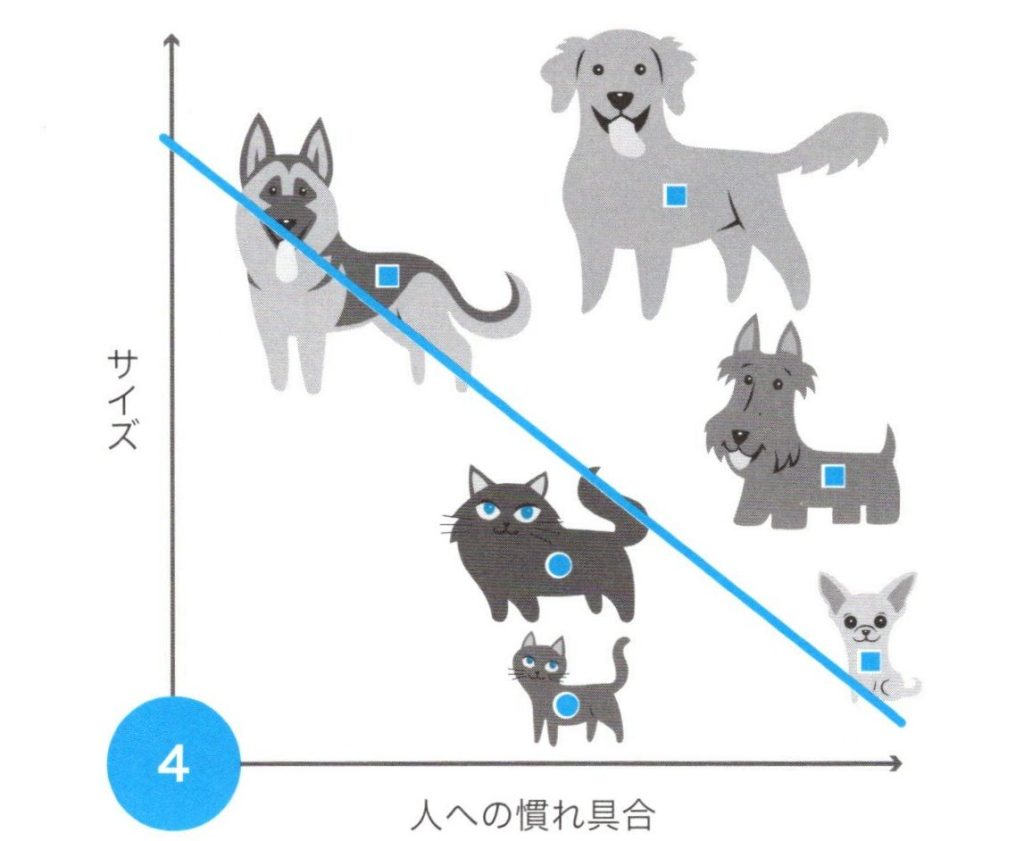
犬と猫の分類(4)
中にはこのような例に当てはまらない犬と猫がいるかもしれませんが、大雑把に1本の直線で綺麗に犬と猫を分離することに成功しました。この様に分類出来ることを、線形分離可能と呼び、実は1つのニューロンでできたパーセプトロンによって学習することが可能になります。
数式で分類を表してみます。入力を、サイズの入力\(x_s\)と体重(kg)で表して0以上100以下、慣れ具合の入力\(s_d\)を0以上10以下の数値で表現し、係数\(w_s\)と\(w_d\)と閾値\(h\)を以下のように定義して適切な値を設定すれば完成です。
Z = \(f(μ)\) = \(f((w_sx_s)+(w_dx_d)-h)\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) (1)
$$
\begin{eqnarray}
Z
=
\begin{cases}
{犬} & {f(μ) > 0 } \\
{猫} & { f(μ) \leq 0 } \tag{2}
\end{cases}
\end{eqnarray}
$$
例えば\(w_s\)=0.1、\(w_d\)=0.1、\(h\)=10などと設定すれば良さそうです。
Z = \(f(μ)\) = \(f((0.1x_s)+(1.0x_d))-10)\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) (3)
この式で、\(x_s\)を50kg、\(x_d\)を8として計算すると\(f(μ)\) = 3となり、0より大きいので犬である、と判定できます。しかしながら、冒頭でも説明したとおり、パーセプトロンで正しく分離・分類出来る問題は、線形分離可能な問題だけです。裏返していうと、非線形な問題には対応できません。非線形な問題とは、下図のようにサイズは小さいが人に慣れていない犬がいた場合などです。
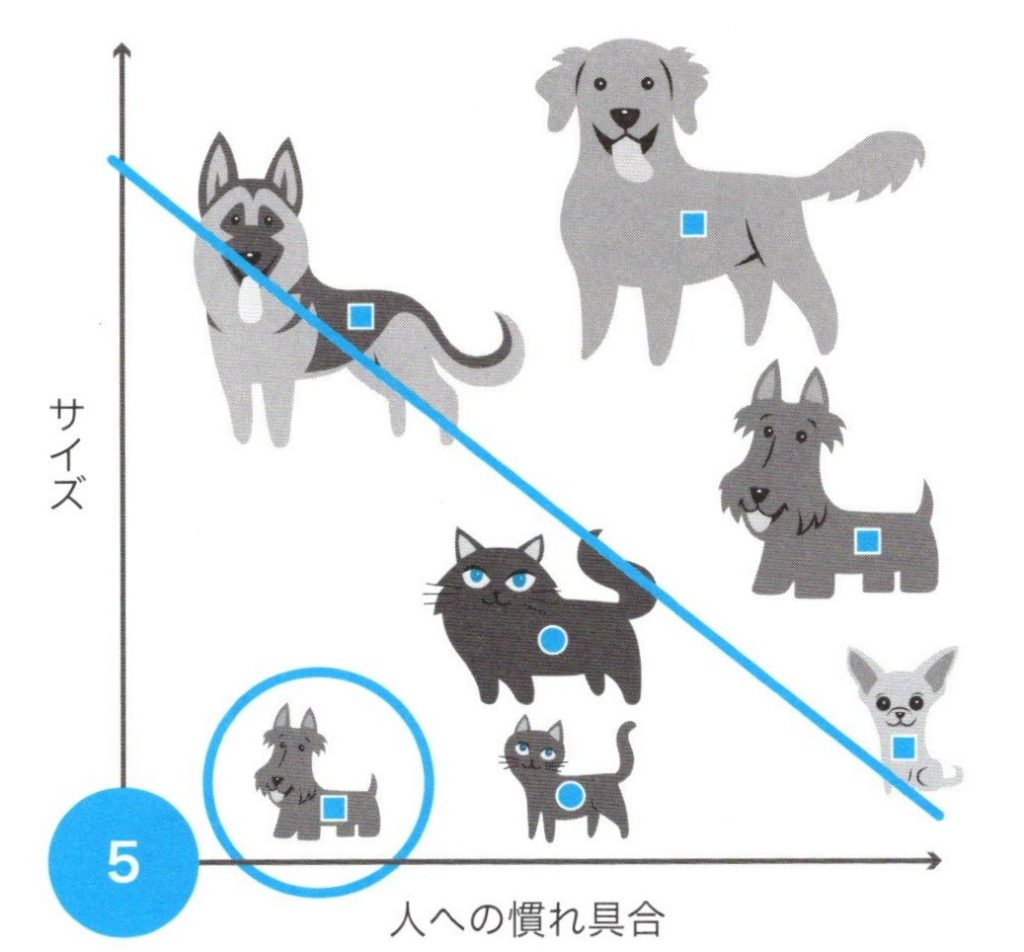
犬と猫の分類(5)
このような場合に、上手く分類できないというわけです。
XOR問題
単純なパーセプトロンでは非線形問題に対応できないことは1988年に指摘されています。非線形問題、具体的には下記表で表せるようなXOR(排他的論理和問題)の場合に対応できません。
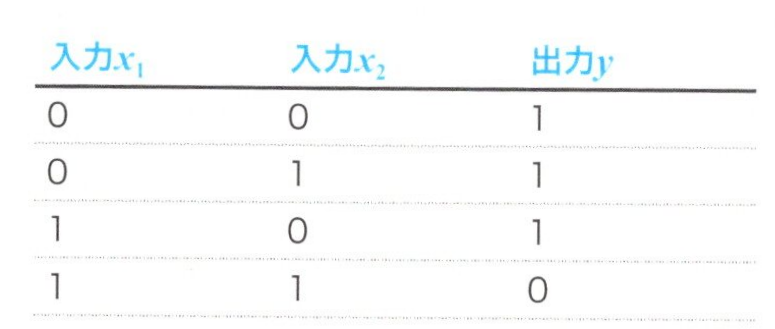
表 XOR問題
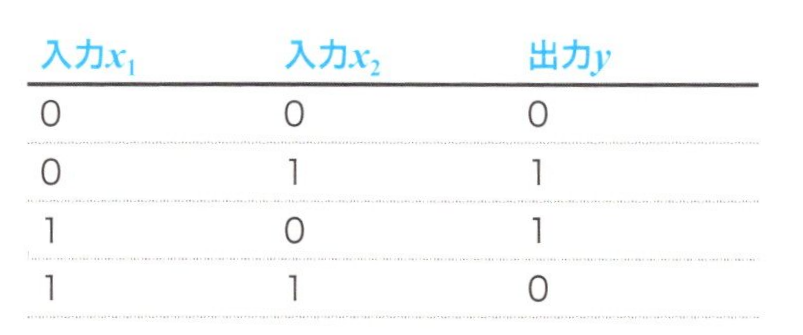
XORは、排他的論理和と呼ばれる論理式のことです。2つの入力\(x_1\)と\(x_2\)に対して、1つの出力yの場合に、次式で表す式のことです。
y =\(x_1\) ⊕\(x_2\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) (4)
0と1の2値の組み合わせを数式に代入すると以下のようになります。
y = 0⊕0 =0
y = 0⊕1 =1
y = 1⊕0 =1
y = 0⊕0 =0
上表は入力と出力の関係を表にしたものです。また、この入力と出力の関係を上手く表現できるように2次元のグラフにすると、下図のようになります。
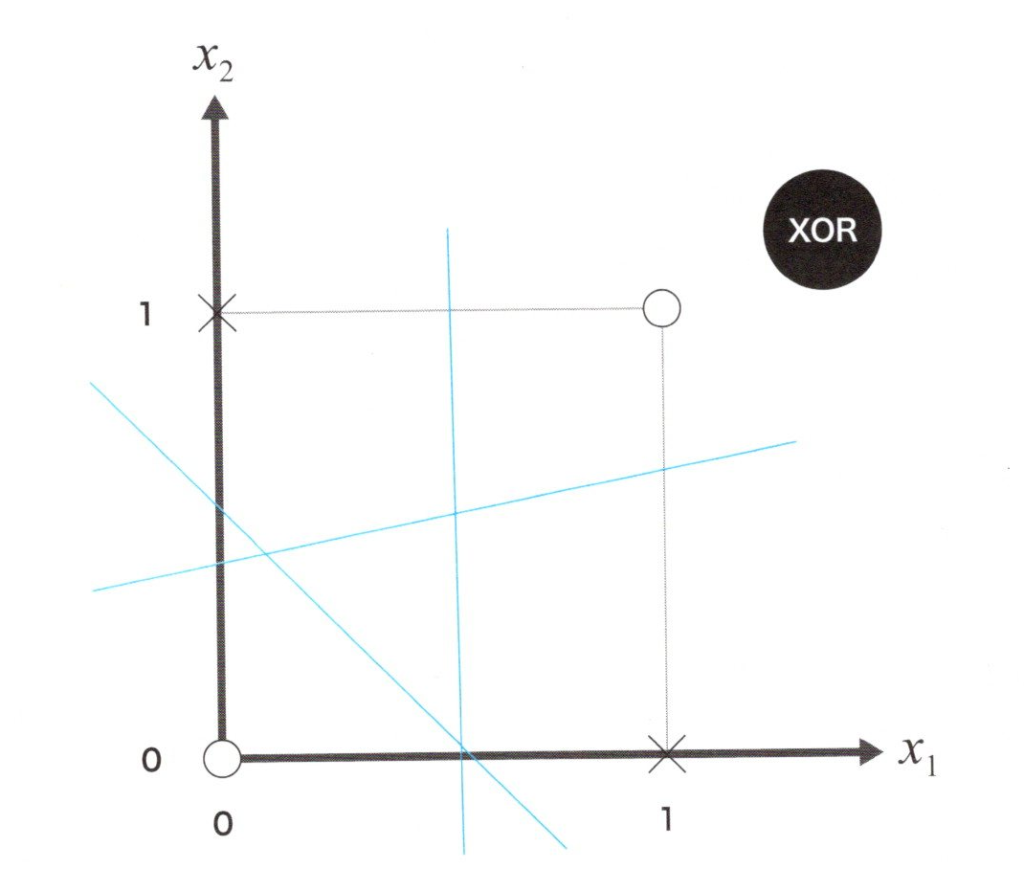
XOR問題
XOR問題は上図のように0と1の組み合わせから0か1の出力を得るという単純な問題なのにも関わらず、2つの部分に別れてしまっているがゆえに、1本の式で区切る方法では分離できません。よって、単純なパーセプトロンは線形分離可能な問題しか扱うことが出来ないため、XOR問題には対応できないというわけです。
多層パーセプトロン(ニューラルネットワーク)
XOR問題は現実の世界でちょっとした矛盾が起こるたびに発生します。例えば犬と猫の分離問題では、サイズと人への慣れ具合を使って分類しようとしましたが、サイズが小さくて人に慣れないのが猫、サイズが大きくて人に慣れるのが犬と分類しようとしても、小さくて人に慣れないような例外的な犬がいると分類しきれないことになります。
このような矛盾した問題にも対応するために、パーセプトロンを階層化することを研究しました。具体的には、パーセプトロンの出力をさらにパーセプトロンに連結するような、多層パーセプトロンと呼ばれるものを研究してきました。一般的には、このような多層パーセプトロンのことをニューラルネットワークと呼びます。
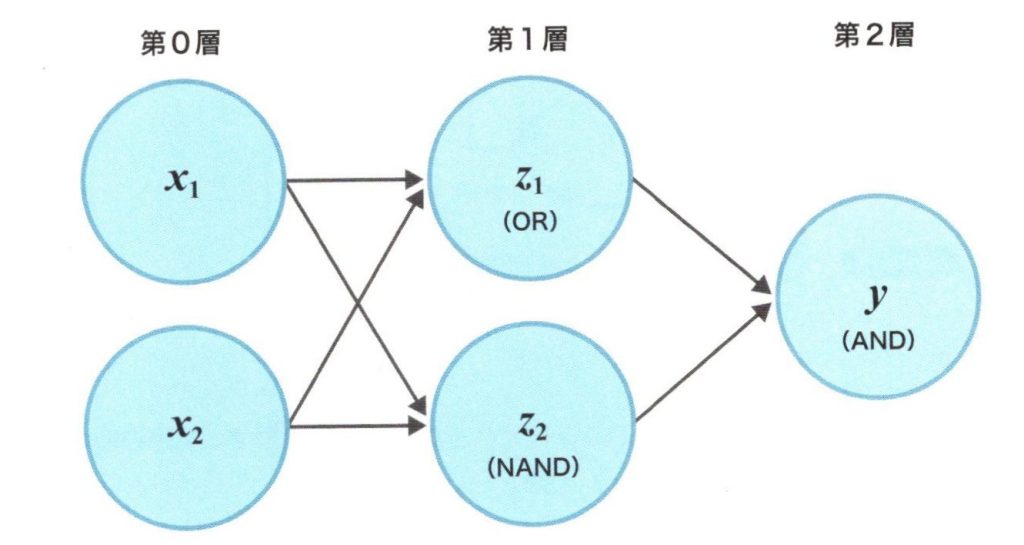
多層パーセプトロン(ニューラルネットワーク)
パーセプトロンを階層化することで、単一のパーセプトロンでは解けなかったXOR問題も解けるようになりました。例えば、上図では中間層(第1層)で\(z_1\)と\(z_2\)を論理演算子のORとNANDの動きになるように学習し、出力\(y\)でANDとなるように学習して結合すれば、入力\(x_1\)と\(x_2\)に対してXOR(排他的論理和)を判定するネットワークを構成することが出来ます。
階層化パーセプトロンでXOR問題を解く

上表は、入力\(x_1\)と\(x_2\)をNANDに入力し、ORの出力\(z_1\)とNANDの出力\(z_2\)をANDの入力として、その出力\(y\)を得る場合の組み合わせを示しています。
このネットワークを論理式で表すと、
$$
\begin{eqnarray}
y = z_1・z_2 = (x_1+ x_2)・\overline{(x_1・x_2)} \tag{4}
\end{eqnarray}
$$
のようになります、さらに論理回路で表すと下図の様になります。
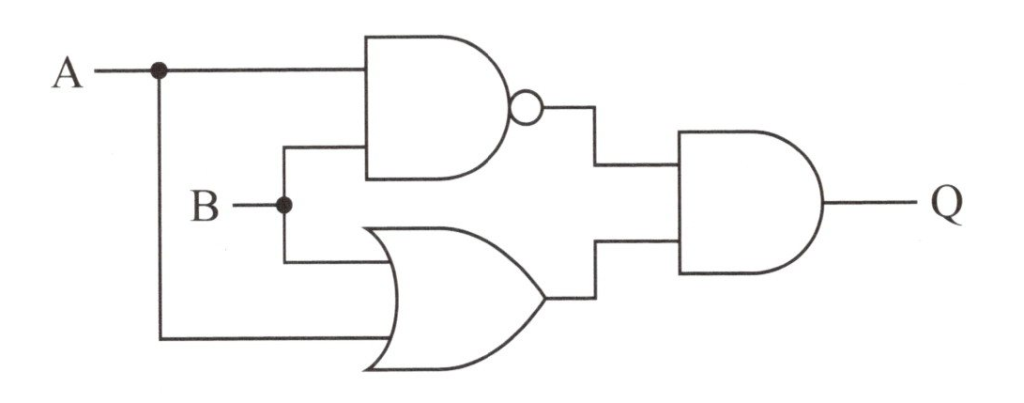
XOR問題を識別する論理回路
XOR問題を識別する論理回路が構成できれば、線形分離できない難しい問題であっても識別可能になります。つまり、XOR回路を構成するOR,NAND,ANDのそれぞれをニューロンで実現すれば良いというわけです。では、より具体的に、OR,NAND,ANDのそれぞれの論理演算子をニューロンで実現するためには、どの様にすれば良いのでしょうか?それについて下記に示します。
OR問題
1つ目のOR問題は、2つの入力が0のときは出力が0、それ以外の入力では1を出力します。言い換えれば入力のどちらかが1であれば出力が1になる論理演算子です。
OR問題
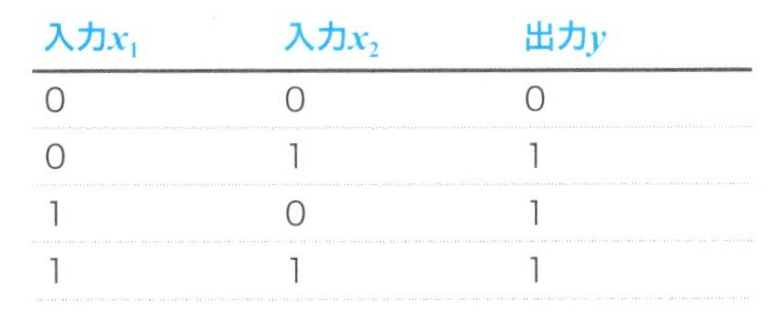
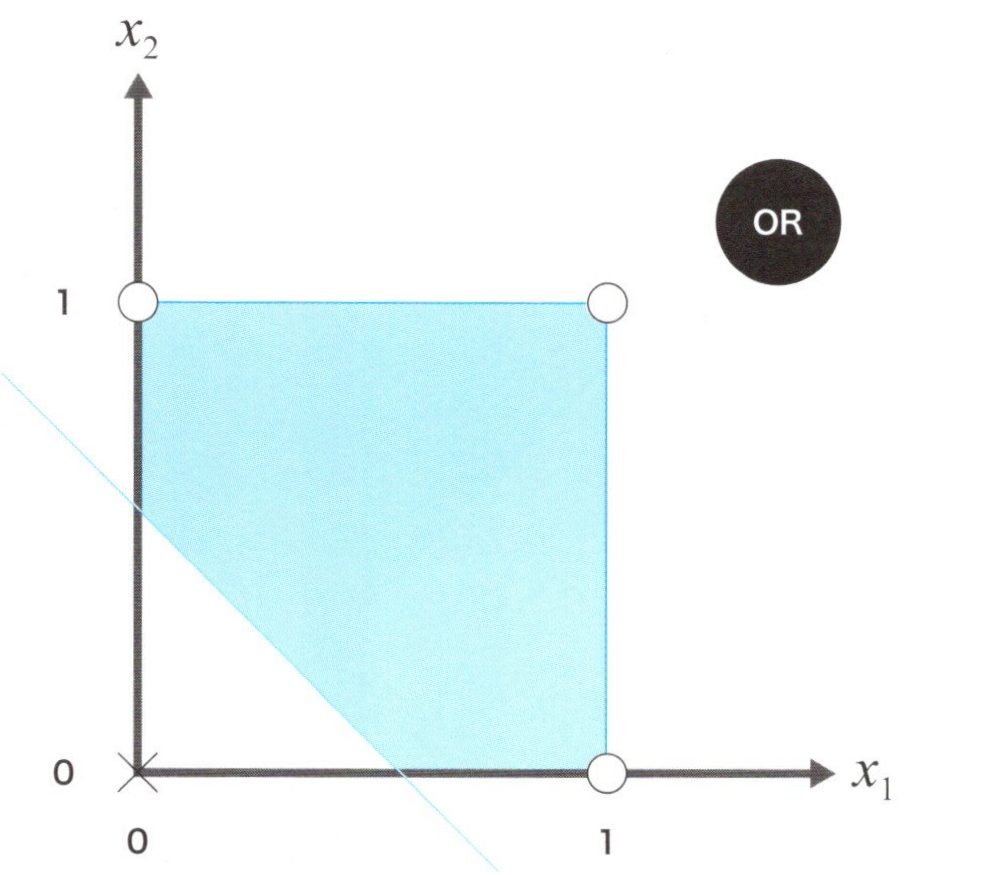
OR問題の識別
Z = \(f(μ)\) = \(f((0.5x_1)+(0.5x_2)-0.2)\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) (5)
この入出力の向き合わせを2次元のグラフにすると、上図のようになります。このグラフでは、青と白の領域に、上手く1本の直線で分離することが出来るため、線形分離可能な問題と言えます。
AND問題
2つ目はAND問題です。2つの入力のうち、その両方が1のときのみ出力が1になる論理演算子です。
AND問題
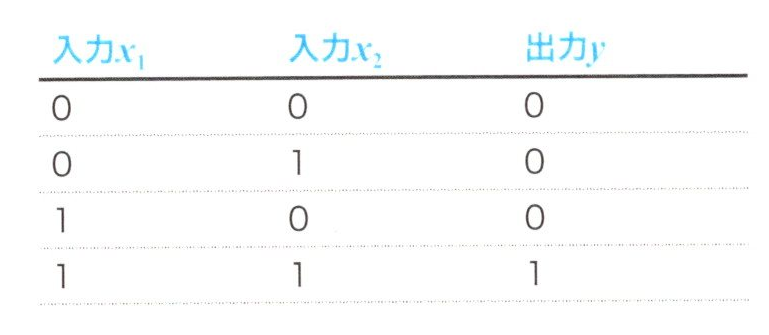
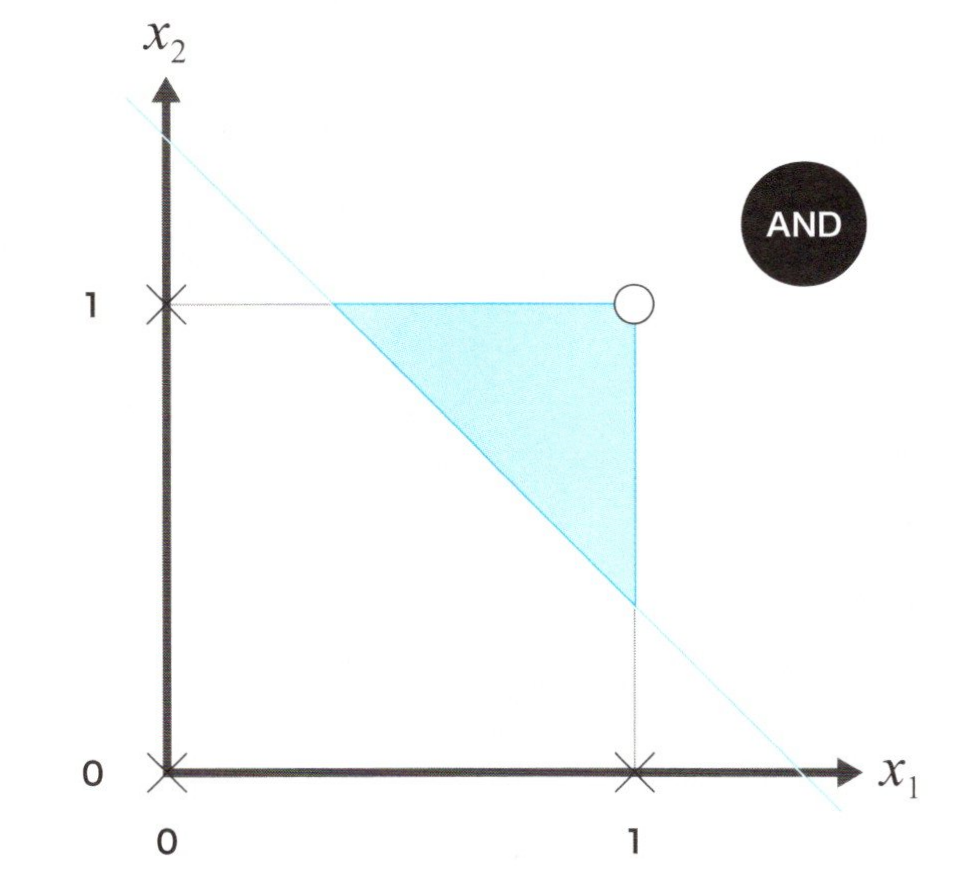
AND問題の識別
Z = \(f(μ)\) = \(f((-0.5x_1)+(-0.5x_2)-0.2)\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) (6)
この入出力の組み合わせを2次元のグラフにすると上図のようになります。このグラフでも青と白の領域を1ほんの直線で分離することが出来るため、線形分離可能な問題と言えます。
NAND問題
3つ目はNAND問題です。両方の入力が1である場合にのみ出力が0になる論理演算子です。
NAND問題
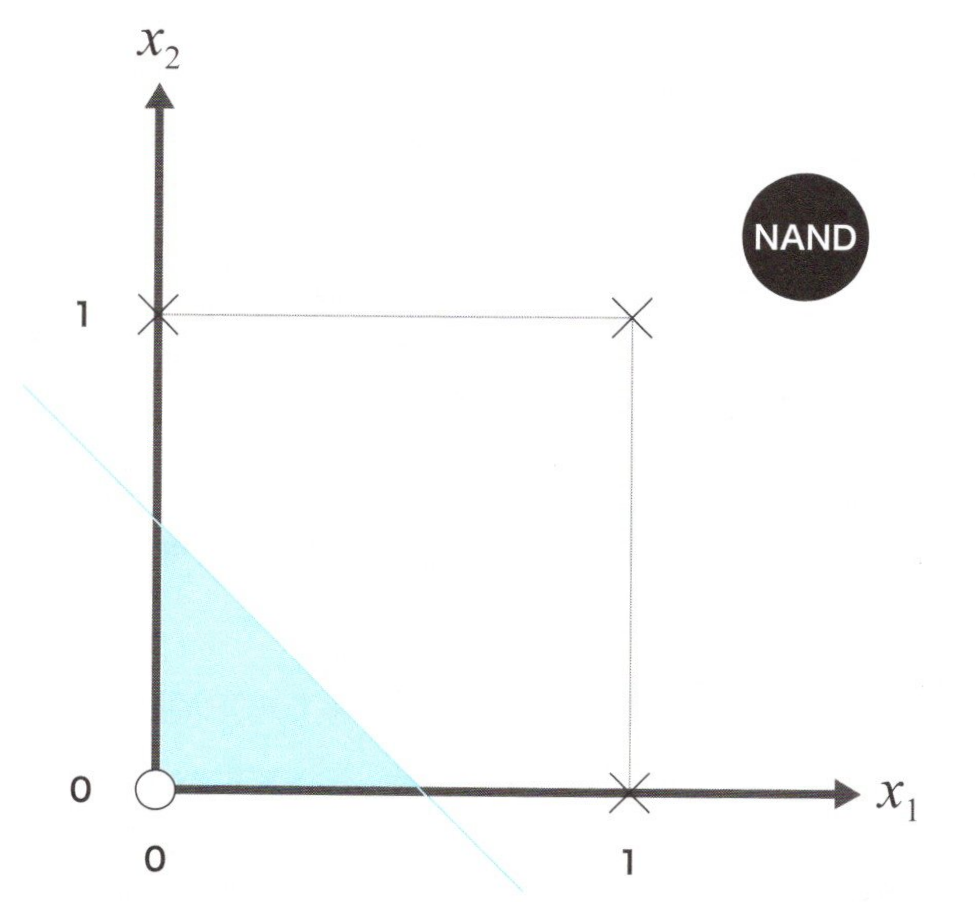
NAND問題の識別
Z = \(f(μ)\) = \(f((0.5x_1)+(0.5x_2)-0.8)\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) \(\qquad\) (7)
この入出力の組み合わせを2次元のグラフにすると上図になります。このグラフでも青と白の領域を1本の直線で分離することが出来るため、線形分離可能な問題と言えます。
ニューラルネットワークでの識別
これまで説明してきたOR,NAND,ANDのそれぞれは線形分離可能な問題でした。つまり、1個のニューロンで識別可能な問題であった、と言えます。
これらのニューロンを組み合わせてネットワークを構成することで、ニューラルネットワークはXOR問題を解決できるというわけです。言い換えると、非線形な問題に対してもニューロンを多層に組み合わせて多重パーセプトロンにすることで、ニューラルネットワークは上手く学習できる、というわけです。
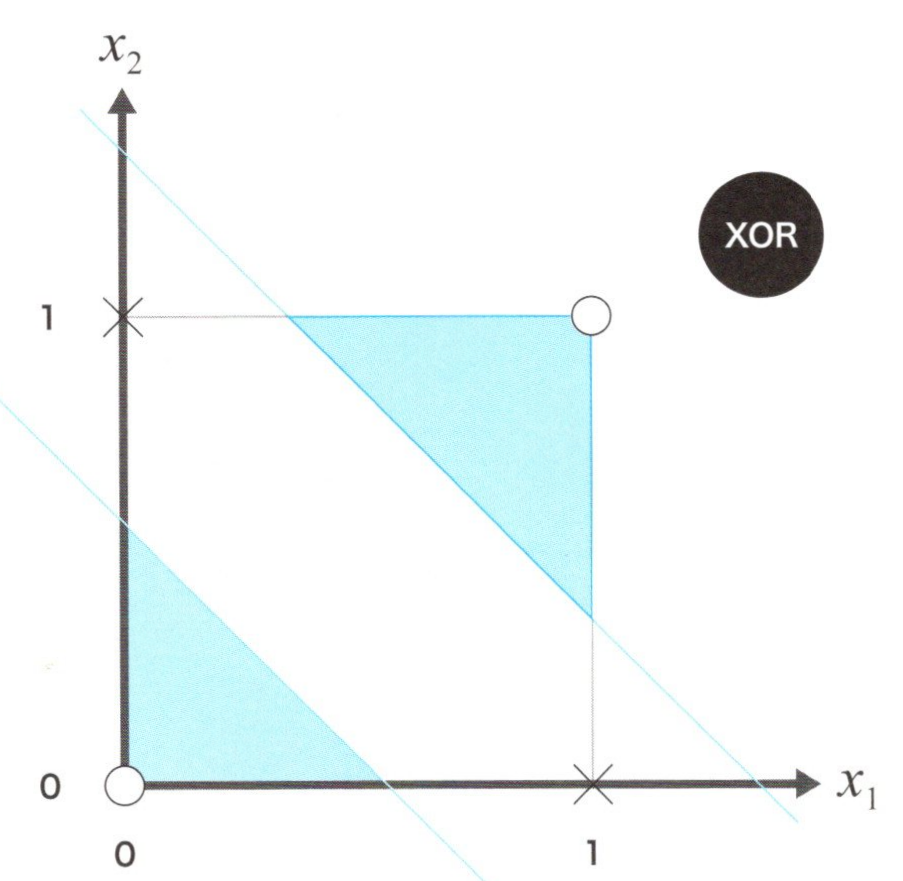
ニューラルネットワークによるXOR問題の識別
上図のグラフは、白の領域が青の領域を分断しており、1本の直線で上手く分離することが出来ないため、線形分離は不可能でしたが、AND,NAND,ORを上手く組み合わせることで2本の直線を使って上手く分離することが出来ました。