活性化関数:ニューロンが入力からの刺激に対して閾値を超えると発火するように、
ある条件を満たす場合は1、そうでないときは0を出力するような
数式であると考えたものを活性化関数と呼びます。
さまざまな活性化関数
前の記事では、ニューラルネットワークの基本素子であるニューロンのモデルを
数式で表し、パーセプトロンと呼ばれている機械学習の仕組みについて触れました。
このモデルの中で、出力であるf(μ)を一番簡単なステップ関数として紹介しましたが、
このような出力関数は、入力によって活性化されることから活性化関数と呼びます。
シグモイド関数
\(\begin{eqnarray}
f(μ)
=
\frac{1}{1+e^{-μ}} \tag{1}
\end{eqnarray}
\)
シグモイド関数は下図のようなf(μ)の値は0以上1以下で、なだらかな曲線を描き
ます。
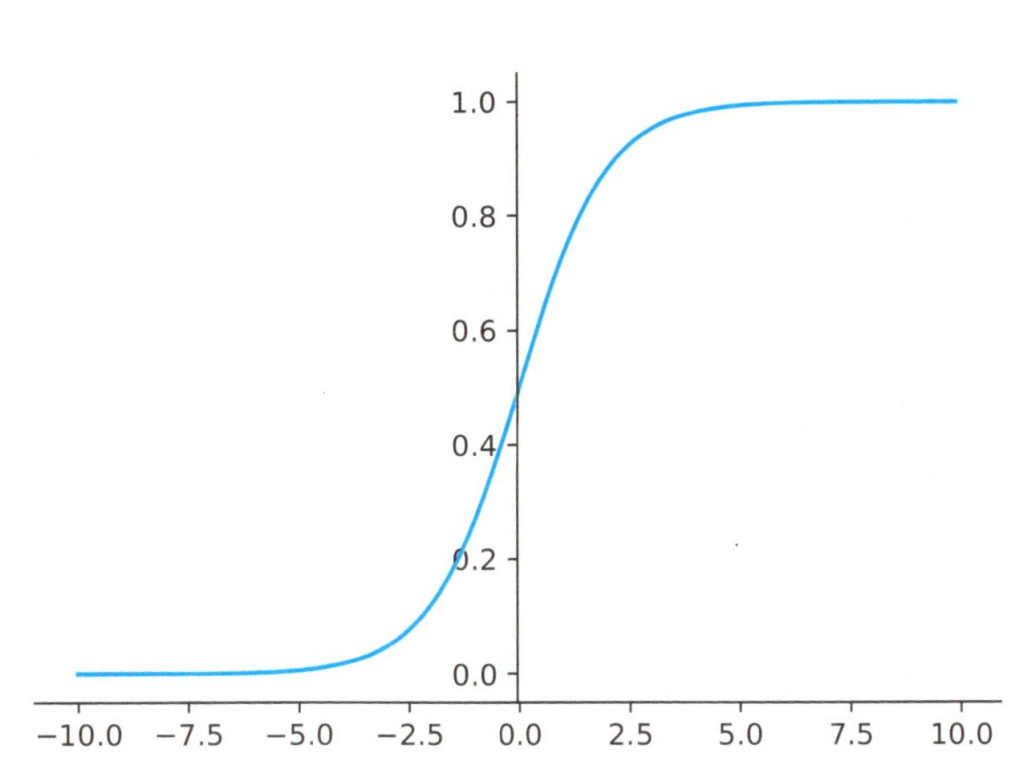
シグモイド関数のグラフ
シグモイド関数をtanh関数(双曲線関数)を用いて表すことも出来ます。下図のように
f(μ)の範囲が-1以上1以下となるところが、通常のシグモイド関数との違いです。
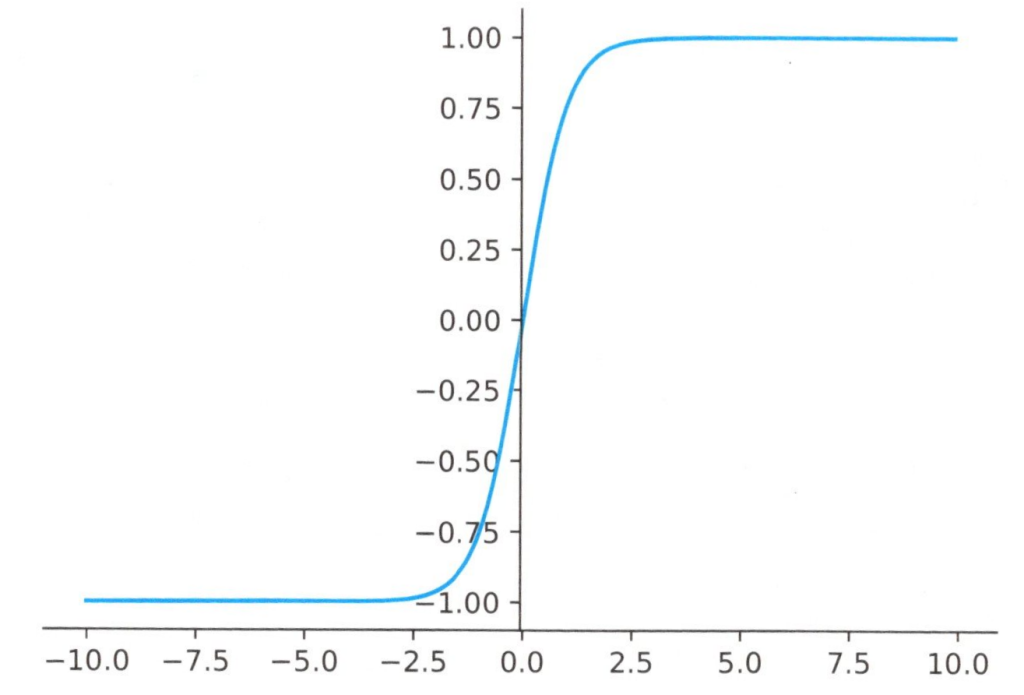
tanh関数(双曲線関数)によるシグモイド関数のグラフ
ReLU関数
\(\)
\begin{eqnarray}
h(x)
=
\begin{cases}
x & ( x > 0 ) \\
0 & ( x \leq 0 ) \tag{2}
\end{cases}
\end{eqnarray}
シグモイド関数は非線形な曲線を描く関数でしたが、もっと簡単な直線を使った
ReUL関数もあります。この関数は下図に示すように線形な関数ですが、0以下なら出力は
0となるのが特徴です。
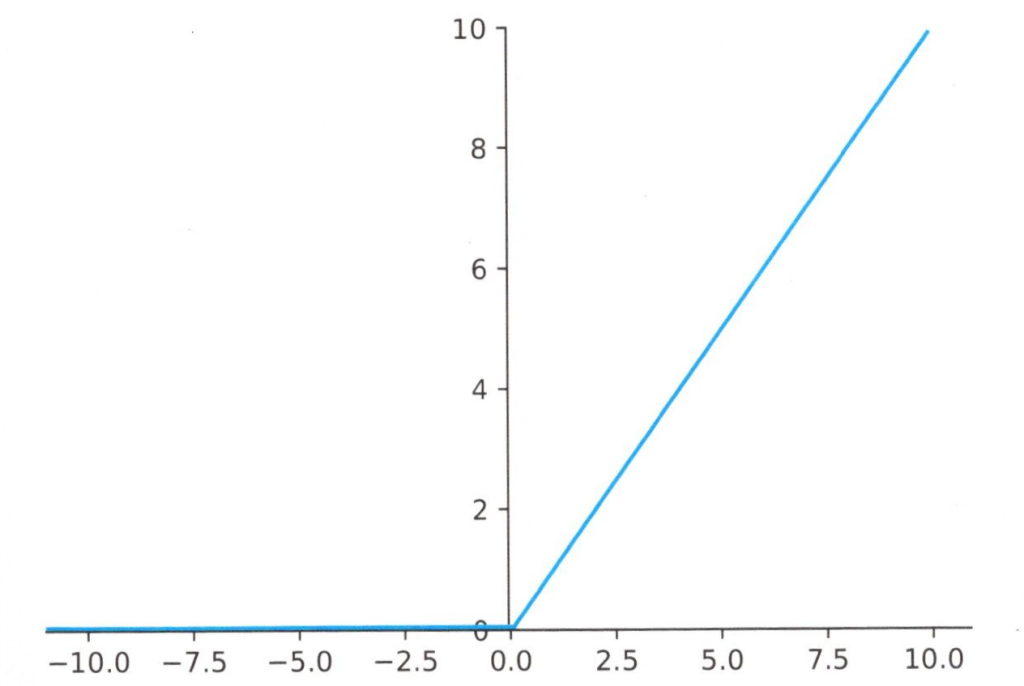
ReUL関数のグラフ