遺伝的アルゴリズム(Genetic Algorithm)とは?
生物進化における遺伝と敵者生存による自然淘汰の仕組みをソフトウェア的に模倣することで、複雑な問題に対する最適解を探索する手法のこと。
具体的には、ある命題に対する解の候補を遺伝子(gene)とその集合である染色体(chromosome)で表現した個体(individual)を複数用意し、適応度(fitness)の高い個体を優先して交叉(crossover)、突然変異(mutation) などの操作を繰り返しながら最適解の探索を行う手法のことです。
遺伝的アルゴリズムのメリットとは?
評価関数の可微分性や単峰性などの知識がない場合であっても適用可能であること、つまり、最適解を求めたい対象に対する他の最適化手法が思いつかなくとも、遺伝的アルゴリズムモデルによって最適解が求められる可能性があります。
遺伝的アルゴリズムに必要とされる条件は、評価関数の全順序性と、探索空間が位相(topology)を持っていることです。
遺伝子の表現の仕方によって、組み合わせ最適化問題やNP困難な問題などの様々な問題に対する適用が可能であることも大きなメリットです。
遺伝的アルゴリズム
1.解を表現する符号化方法を決定する。
2.N個のランダムな個体を含む集団を用意する。これを「現世代」と呼ぶ。
3.N個の個体を格納可能な集団を用意する。これを「次世代」と呼ぶ。
4.評価関数を用いて、現世代の各個体の適応度をそれぞれ計算する。
5.ある確率で次の3つの操作を行い、その結果を次世代に保存する。
1)全世代から2つの個体を選択する。
2)選択された個体を用いて交叉を行い、子孫(offspring)を生成する。
3)交叉によって生成された子孫に対して、突然変異を適用する。
6.次世代の個体数がN個になるまで5の操作を繰り返す。
7.次世代を現世代に移行し、命題が収束するまで3〜6の手順を繰り返す。
この結果を「最終世代」と呼ぶ。
命題の収束を判定する方法として、以下のような場合が求められる。
・集団中の最大適応度が、ある閾値よりも大きくなった場合
・集団中の平均適応度が、ある閾値よりも大きくなった場合
・集団の適応度増加率が、ある閾値以下の世代が一定期間続いた場合
・世代交代の回数が規定の最大世代数に達した場合
8.最終世代の中で最も適応度の高い個体を「解」として出力する。
染色体エンコードについて
染色体エンコードとは、解の特徴を遺伝子として表現することです。
エンコード手法とその詳細を下記に示します。
・バイナリエンコーディング(binary encording)
各遺伝子を0,1のビットとして表現する符号化方法
例:染色体A 1001011101101
染色体B 1010011010111
・順列エンコーディング(permutation encording)
各遺伝子を順列を示す数字として表現する符号化方法
→巡回セールスマン問題や仕事の順序などの並び替え問題の表現に用いられます。
例:染色体A 276418359
染色体B 461957382
・実数値エンコーディング(real encording)
各遺伝子を数値(または文字)として表現する符号化方法
→実数値データなど、バイナリエンコーディングでは表現が難しい場合に用います。
例:染色体A 0.51 2.83 3.12 1.50
染色体B AGTCATGCAGCATTA
染色体C 前進 前進 右 後退 左
・木構造エンコーディング(tree encording)
染色体を1本の紐(配列)ではなく、木構造データとして表現する符号化方法
→遺伝的プログラミングや進化的プログラムなどの表現に用いられています。
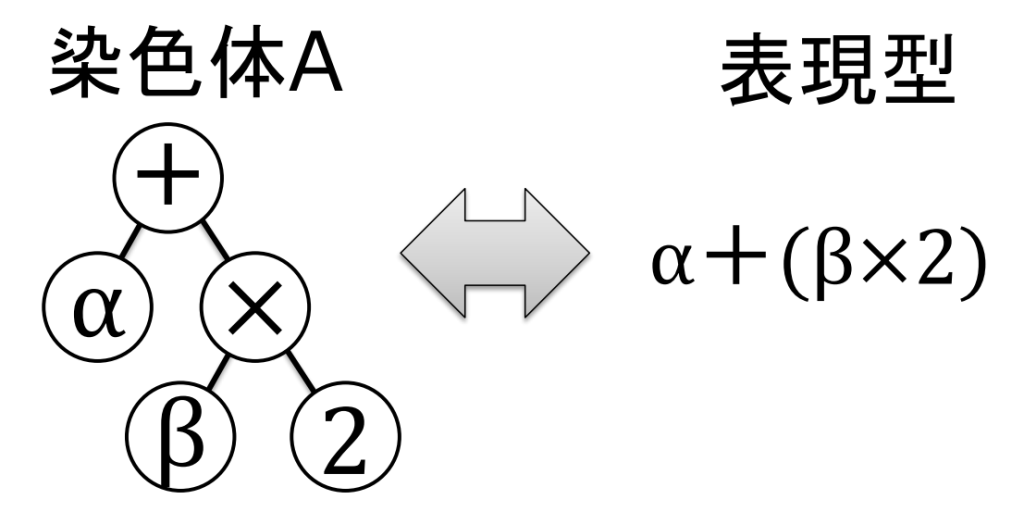
染色体エンコードの例
・ナップザック問題(Knapsack Problem)
容量\(C\)のナップザックが1つと、各々の価値が\(P_i\)、容積が\(C_i\)であるところの\(n\)個の品物\(E_i\)が与えられた時、\(C\)を超えない範囲でいくつかの品物をナップザックに詰め、入れた品物の価値の和を最大化するにはどの品物を選べばよいか。
この問題をバイナリエンコーディングで表現してみます。
\(n\)個の荷物 → 遺伝子長(\(L\)) = \(n\)
\(i\)番目の荷物 → 遺伝子座(\(p\)) = \(i\)
荷物\(E_i\)を入れる → 遺伝子[\(i\)] _= 1
荷物\(E_i\)を入れない → 遺伝子[\(i\)] = 0
適応度 → 持っている荷物の総価値
以上を纏めると、ナップザック問題は以下のように表現できます。
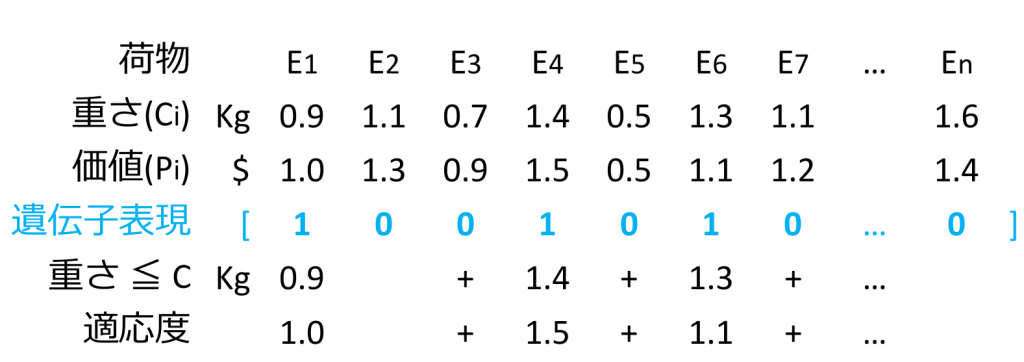
ナップザック問題をバイナリエンコーディングで表現
・循環セールスマン問題(Travelling Dalesman Problem)
\(n\)個の都市\(C_i\)と、それぞれの都市間の距離\(D_{i,j}\)が与えられているとき、最初の都市を出発し、全ての都市を経由して、同じ都市に戻ってくるルートのうち、最短のルートを求めよ。
この問題を順列エンコーディングで表現してみます。
\(n\)個の都市 → 遺伝子長(\(L\)) = \(n\)
\(i\)番目に訪れる→ 遺伝子座(\(p\)) = \(i\)
荷物\(C_x\) → 遺伝子[\(i\)] _= x
適応度 → 循環ルートの総距離
以上を纏めると、循環セールスマン問題は以下のように表現できます。
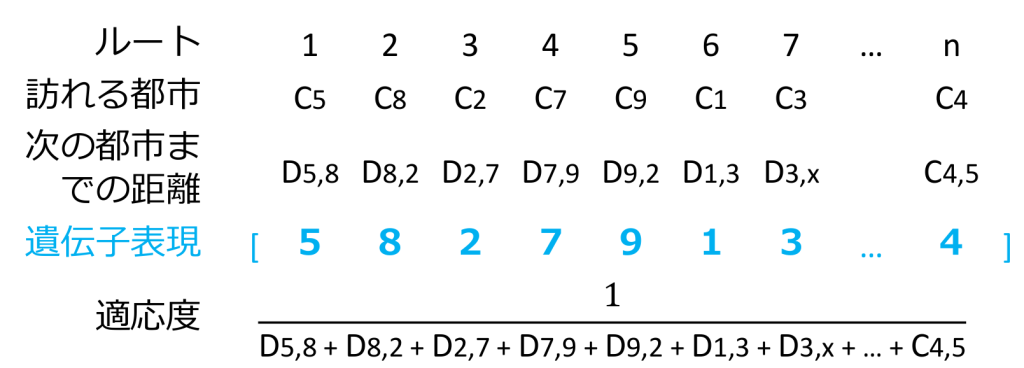
循環セールスマン問題を順列エンコーディングで表現