ディープラーニングの応用の1つである自然言語処理について詳しく見ていきます。このレッスンでは、再帰型ニューラルネットワークを用いて自然言語を理解する方法について紹介します。
RNNの特徴
再帰型ニューラルネットワーク(RNN:Reccurent Neural Network)は、多層のニューラルネットワークの各階層の出力を、その階層の入力にそのまま戻るような自己ループ(Self-Loop)を追加している、という特徴を持ちます。このネットワーク構造にすることで、前の改装の入力を記憶することが出来、入力データが長いシーケンス(連続値)だったとき、注目するデータの前に入力されたデータの意味を考慮できるようになります。
下図(a)はシンプルなRNNの構造です。単純な再帰型ニューラルネットワークは、下図(b)の2層ニューラルネットワークに非常に似ています。
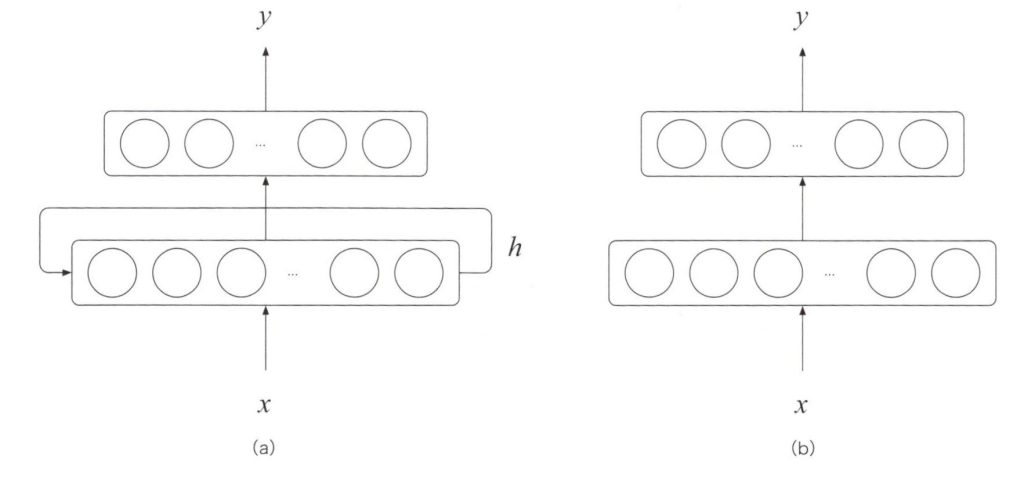
RNN層と2層ニューラルネットワークの比較
このネットワークは、入力ベクトル\(x\)に対して出力ベクトル\(y\)を生成します。これまでとの違いは、最初の階層に自己ループが追加されていることです。2層ニューラルネットワークと同じように、第1層の出力\(h\)は第2層へ受け渡され、出力ベクトル\(y\)が生成されます。2層ニューラルネットワークと違って、\(h\)は同時に第1層の入力としても受け渡されています。このベクトル\(h\)が、再帰型ニューラルネットワークの内部状態(Inner State)を保持していると考えます。
・RNNにおける情報の展開
下図の(a)のような再帰型ニューラルネットワークの自己ループは、下図(b)のように展開された2層ニューラルネットワークの上を、一連の情報が流れるような道を構築することに相当します。なぜこのように展開できるのかを簡単に説明しますと、再帰型ニューラルネットワークは、表面的には1つの四角い形状のニューロンの層に、次のニューロンの入力に情報を受け渡すためのニューロンを隠しています、実際には同じ層を使うわけですから、展開されたニューラルネットワークのパラメータは、階層ごとに同じ値です。入力ベクトル\(x_t\)はある時点step\(t\)における外部からの入力データ、ベクトル\(h_{t-1}\)は\(x_t\)が入力される前の再帰型ニューラルネットワークの内部状態を表すベクトルです。再帰型ニューラルネットワークは、この\(x_t\)と\(h_{t-1}\)とに基づいて\(h_t\)で表す第1層の内部構造を更新し、step\(t\)における内部状態ベクトル\(h_t\)に基づいて出力ベクトル\(y_t\)を生成します。
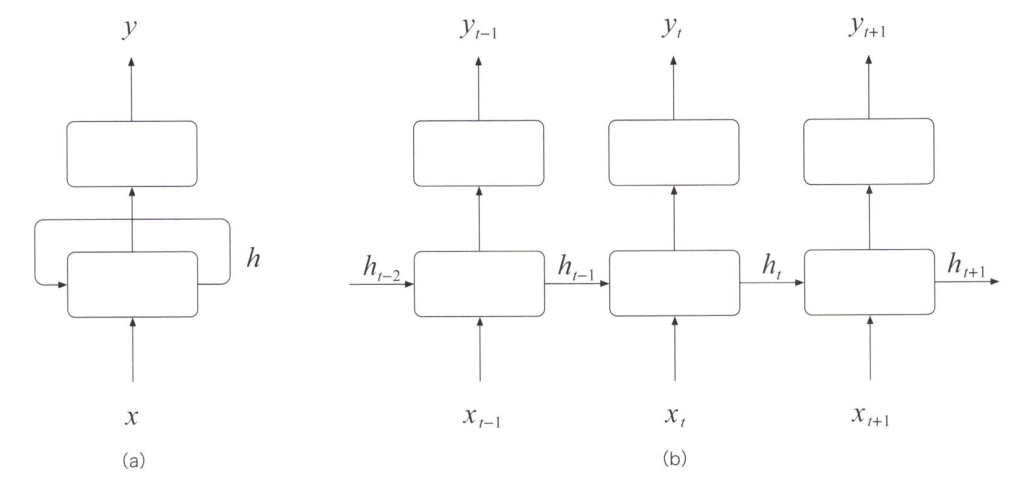
再帰型ニューラルネットワークとその展開図
単一のニューロンは、この文章に品詞のラベルを付けるために上図(b)の再帰型ニューラルネットワークを使うことを考えてみます。ある時点step\(t\)に入力された文章を入力ベクトル\(x_t\)としたとき、この\(x_t\)に対応する出力ベクトル\(y_t\)を品詞ベクトルとします。
再帰型ニューラルネットワークの内部状態\(h_{t-1}\)は、step\(t\)より前に理解して記憶した情報を保持しています。文章の断片\(x_0\),\(x_1\),・・・,\(x_{t-1}\)に自然言語として意味があると考えて、step\(t\)の時点で、再帰型ニューラルネットワークが文章の断片\(x_t\)を読み込み、\(x_t\)と\(h_{t-1}\)に基づいて内部構造\(h_t\)を更新します。これと同時に、品詞ラベル\(y_t\)の確率が新しい内部状態\(h_t\)に基づいて求められます。
RNNの柔軟性
再帰型ニューラルネットワークは、非常に柔軟性があります、最初のstep0以外では、入力\(x\)を必要としないネットワークや出力ベクトル\(y\)がステップごとに毎回生成されないネットワークも構成できます。下図は異なるタスクに対応するさまざまな再帰型ニューラルネットワークの例です。
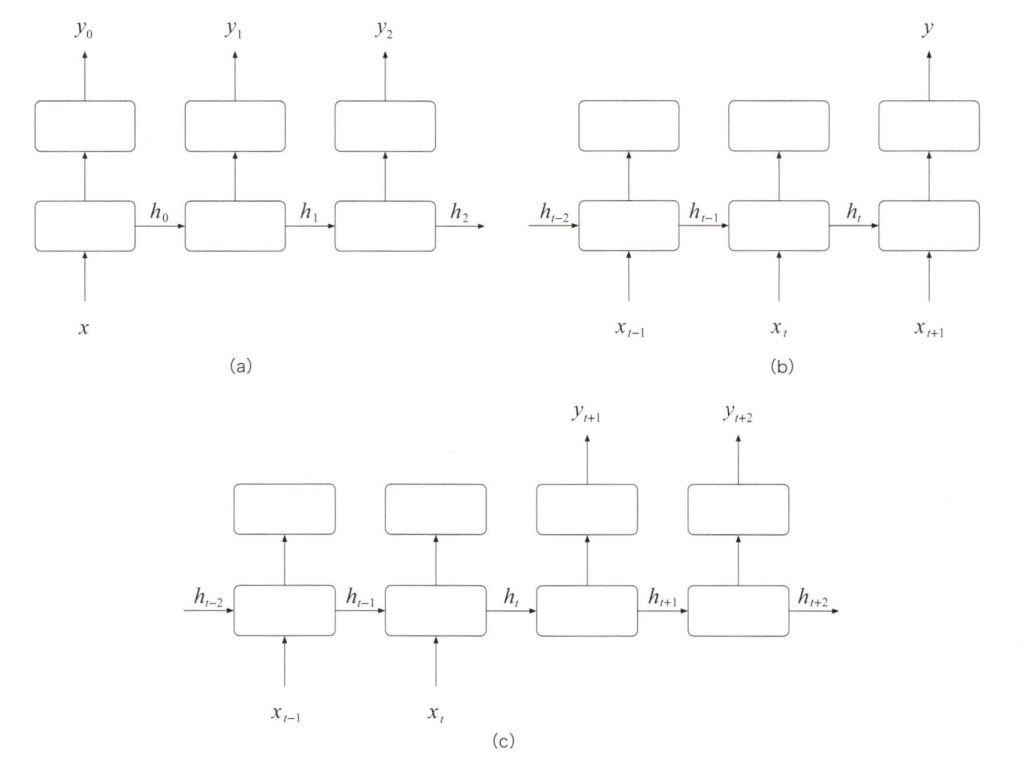
再帰型ニューラルネットワークのいろいろ
例えば、上図(a)のRNNは辞書のように1語の単語の説明を生成するネットワークです。1語の入力\(x\)に対して、出力ベクトル\(y_0\),\(y_1\),・・・が得られます、次に上図(b)のRNNは感情極性ラベル(Sentiment Label)を推測するネットワークです。単語例(Word Sequence)の入力ベクトル\(x_0\),\(x_1\),・・・に基づいて、正または負(Positive or Negative)の出力\(y\)を得られます。上図(C)のRNNは、日本語の文章を入力ベクトル\(x_0\),\(x_1\),・・・\(x_t\)として、出力ベクトル\(y_0\)、,\(y_1\),・・・として英語の文章に翻訳できます。
最も単純な計算モデル
単純な再帰型ニューラルネットワークの計算モデルをコンパクトにまとめた図は、下図になります。
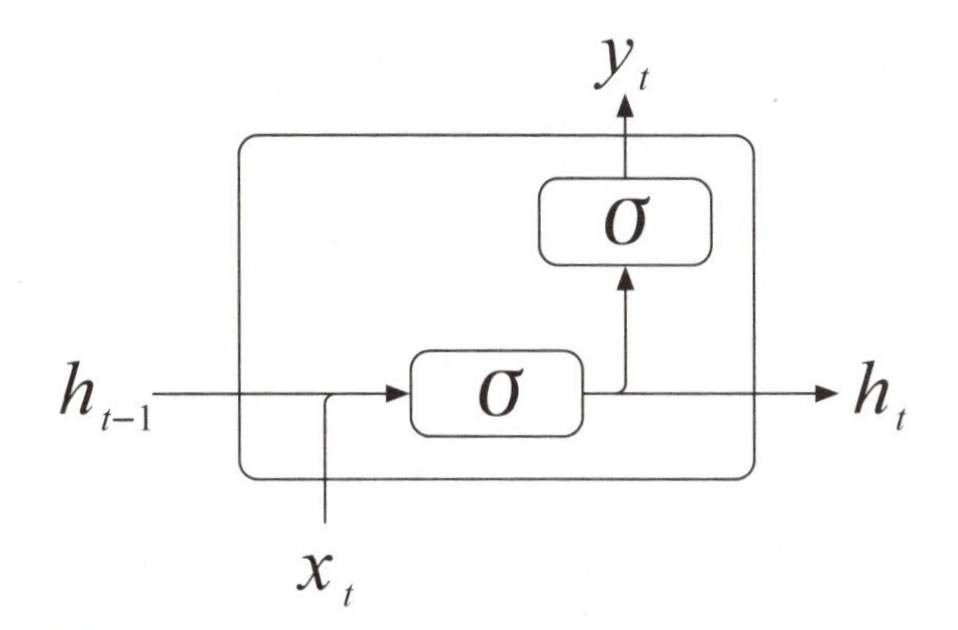
最も単純な再帰型ニューラルネットワークの計算
step\(t\)の時点の入力ベクトル\(x_t\)と、更新前の内部状態ベクトル\(h_{t-1}\)は連結されて[\(x_t\),\(h_{t-1}\)]形状の長いベクトルになり、これを入力として活性化関数\(σ\)の出力を内部状態ベクトル\(h_t\)とします。
\(\begin{eqnarray}
h_t
=
σ(W_h ✕ [h_{t-1},x_t] ) \tag1
\end{eqnarray}
\)
新しい内部状態モデル\(h_t\)は、次のステップへ内部ループを経由して受け渡されると同時に、第2層の全結合層では、活性化関数\(σ\)を使って、step\(t\)の時点の出力ベクトル\(y_t\)が得られます。
\(\begin{eqnarray}
y_t
=
σ(W_h ✕ h_t) \tag2
\end{eqnarray}
\)
水平に並んでいる\(h_0\),\(h_1\),・・・,\(h_t\)は事前の入力\(x_0\),\(x_1\),・・・,\(x_{t-1}\)を統合した情報を表します。この特徴的な方法により、RNNは過去の情報を記憶します。