勾配法は、最適化問題に落とし込めることを前の記事で触れました。この最適化問題は機械が最適解を見つける方法論であり、機械学習であるといえます。この方法論を利用すればデルタ則に従ってニューロンの1つ1つが学習できる、というわけです。しかしながら、ニューロン1個では線形な問題にしか対応出来ず、非線形な問題には対応できないことは前述しました。
誤差逆伝播法とは?
ニューロン1個や単相のパーセプトロンでは学習しきれない、非線形な問題を学習するための方法として、多層パーセプトロン=ニューラルネットワークが提案されましたね。それでは、複数のニューロンが連結して構成されたニューラルネットワークの場合はどの様に学習すれば良いでしょうか。現在、最も有効な学習方法の一つとして、誤差逆伝播法(バックプロパゲーション)が提案されており、ニューラルネットワークの学習に採用されています。
誤差逆伝播法は、「誤差を 逆に 伝搬する」方法です。ニューロン1個のときは下図のような仕組みです。
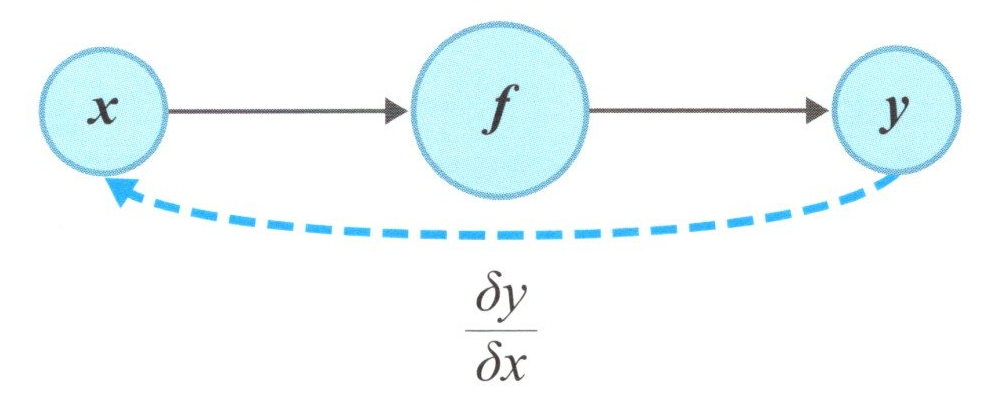
1層の誤差逆伝播
連鎖律
ニューロン1個では、比較的単純で線形な問題にしか対応できませんでしたが、ニューロンを複数個利用して階層化することで、複雑で非線形な問題にも対応できるようになります。この時、ニューロラルネットワーク全体を学習するための方法が、誤差逆伝播です。誤差逆伝播の肝となる数学的な理論に、連鎖律(Chain Rule)というものがあります。
下図のように、ニューラルネットワークが1個のニューロンの場合は、更新式(傾き)は、以下の様に表せます。
更新式(傾き)=\(\frac{ dy }{ dx }\) (1)
さらにニューロンを増やして下図のように階層を深くしていくとどうでしょうか。
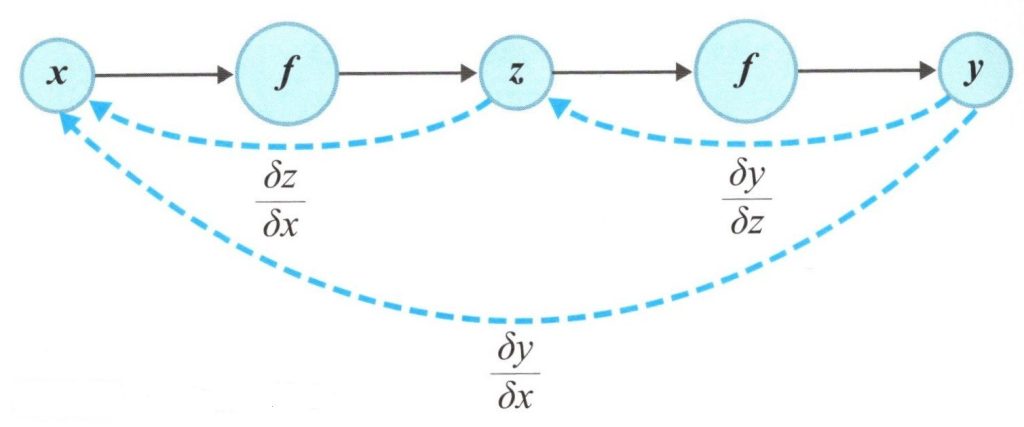
2層の誤差逆伝播
数学的には、微分(偏微分)すればこの傾きを求めることが出来ますが、それをさらに連結した隣のユニット(ニューロン)へ伝播することをバックプロパゲーションや逆伝播といわれるものです。
更新式(傾き)=\(\frac{ dy }{ dx }\) = \(\frac{ dy }{ dz }\) \(\frac{ dz }{ dx }\) (2)
この式の様に、誤差に対して重みの更新をするための更新式を、連鎖的に求めることが出来ます。これを連鎖律と呼びます。実際には、もっと複雑なネットワーク構造であったり、難しい偏微分を説いたりする必要がありますが、ニューラルネットワークでは、活性化関数\(f\)や、損失関数\(E\)に微分可能な式を採用することで、ニューラルネットワーク全体を逆伝播する際の更新式の偏微分を行えるように工夫しているのです。