前の記事では二乗和誤差や交差エントロピー誤差を使って、ニューラルネットワークの学習の度合いを評価する方法について説明しました。では、その誤差を使ってどの様にニューラルネットワークjのパラメータを調整すれば良いのか、本記事で触れます。
パラメータはどう調整する?
何も工夫をしないのであれば、とにかくいろいろな値を投入し、誤差が最も小さくなるところを探せばよいのですが、パラメータの数が多いと、その組み合わせの数は膨大なので、手当り次第、というのはよくなさそうです。
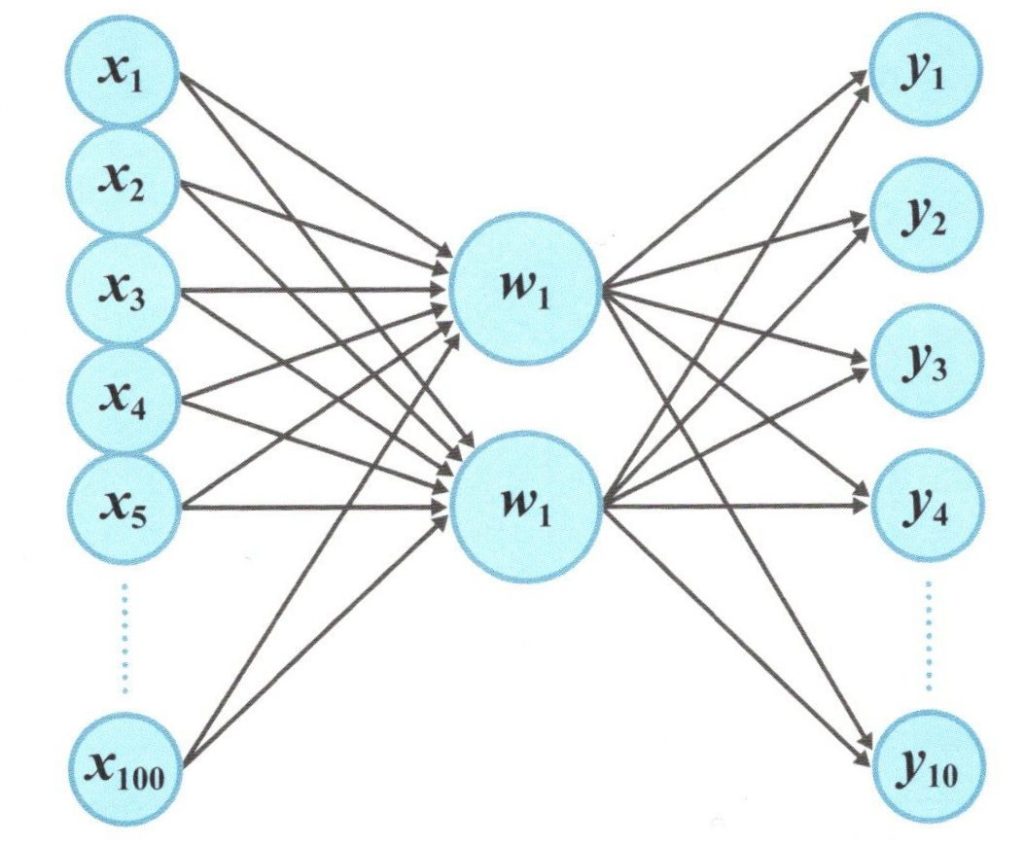
ユニット数2の単相ニューラルネットワーク
上図のように、入力データ\(x\)の次元が100、出力データの次元が10の時、ニューラルネットワークの階層が1層で、ユニット(ニューロン)がたかだか2つしかない場合でも、
100✕2✕10=2000
となり、2000通りのパラメータの組み合わせを、それぞれのパラメータの数値の範囲で試さなければならないことになります。この様に、膨大な数の組み合わせでの最適解の導出には時間がかかってしかたありません。そこで登場するのが勾配法(gradient method)です。勾配法は”傾き”を利用した方法です。
わかりやすく勾配方の考えのイメージを説明すると、「世界一高い山を目指そう」と考えた時、空から計測するとか、三角測量や測定器などを利用することが出来ない場合にどうするか? を考えるとイメージしやすいです。私なら、まずは近場の山の頂上を目指して上り、頂上についたらさらにもっと高い山がないか、次の山を目指して隣の山を登ります。
こうして頑張って探し続けていれば、いつかは世界一高い山を見つけることは不可能ではないと考えられます。この「頂上を目指して登る」という部分が勾配法となります。
ニューラルネットワークを含む機械学習アルゴリズムでは、この勾配法を用いて誤差が最小になるようなパラメータを求めます。これを誤差最小問題と呼びます。最小化問題の場合の勾配法を勾配効果法や最急降下法ともいいます。
ニューラルネットワークの誤差の勾配の求め方
では、ニューラルネットワークの誤差の勾配(傾き)はどうやって求めたらよいか?という内容についてこのトピックで触れます。
結論から述べますと、微分(偏微分)を利用して微分値が0になる値を求めます。
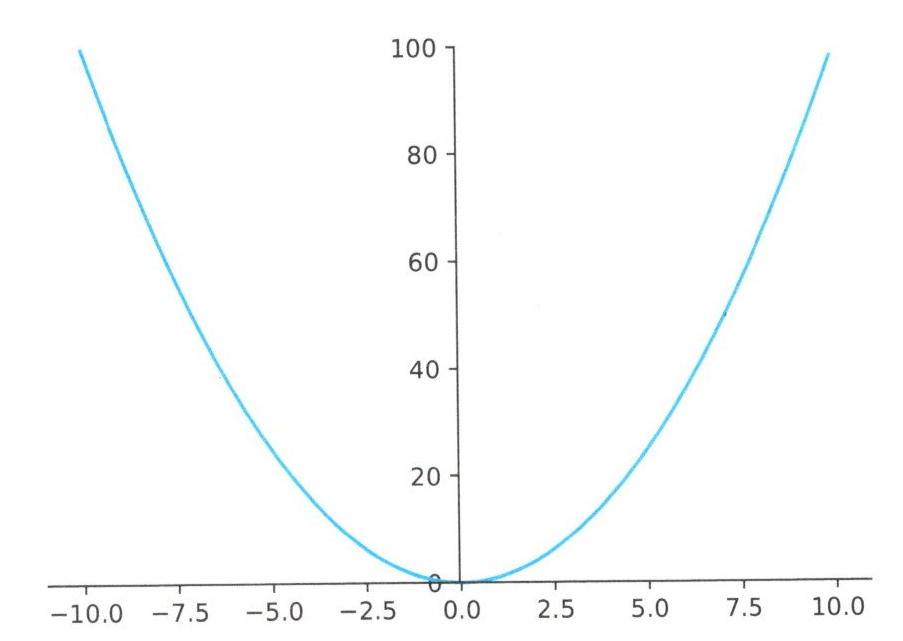
y = \(x^2\)のグラフ
しかし、もし微分が上手く出来なかったり、いろいろな関数が組み合わさっていて単純に微分した値が0になるところを求められない場合はどうでしょうか?なんとかして最小値を求めなければならないので、実際に値\(x\)を変えてみて、最小となる\(y\)を見つけようと思います。この時、ある点、例えば\(x\)=6付近の傾きがわかればその続きの下の方に向かうように、\(x\)の値を変更すれば良いことがわかります。下図で、その様子を図示しています。
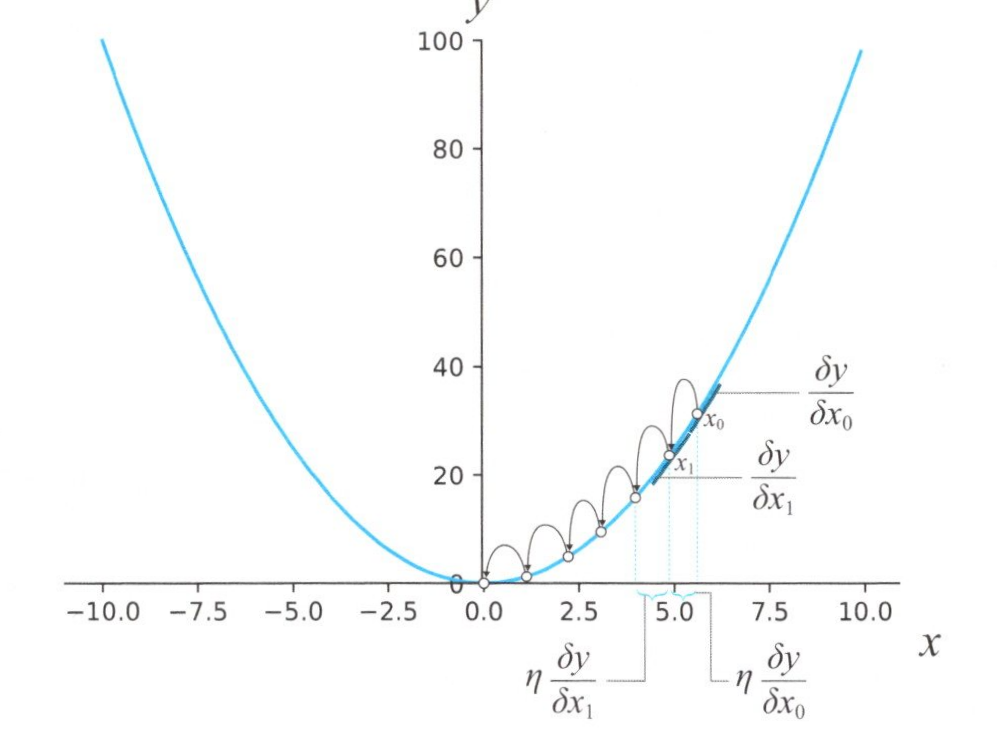
最小値を探す
各地店での傾きを数式で表すと、次のようになります。
\(x_1\)=\(x_0\)-\(η\)\(\frac{ dy }{ d{x_0}}\) \(\tag{1}\)
\(x_2\)=\(x_1\)-\(η\)\(\frac{ dy }{ d{x_1}}\) \(\tag{2}\)
この式に出てくる\(η\)は学習係数と呼ばれていますもので、人間が山登りをする例でいうと、歩幅に相当するものです。小さい幅にすると小走りなので遅くなりますが、大きすぎる値にすると下図のように、大股でジャンプしてしまって、最小値(解)を通り過ぎてしまう可能性もあるので、慎重に調整が必要となります。
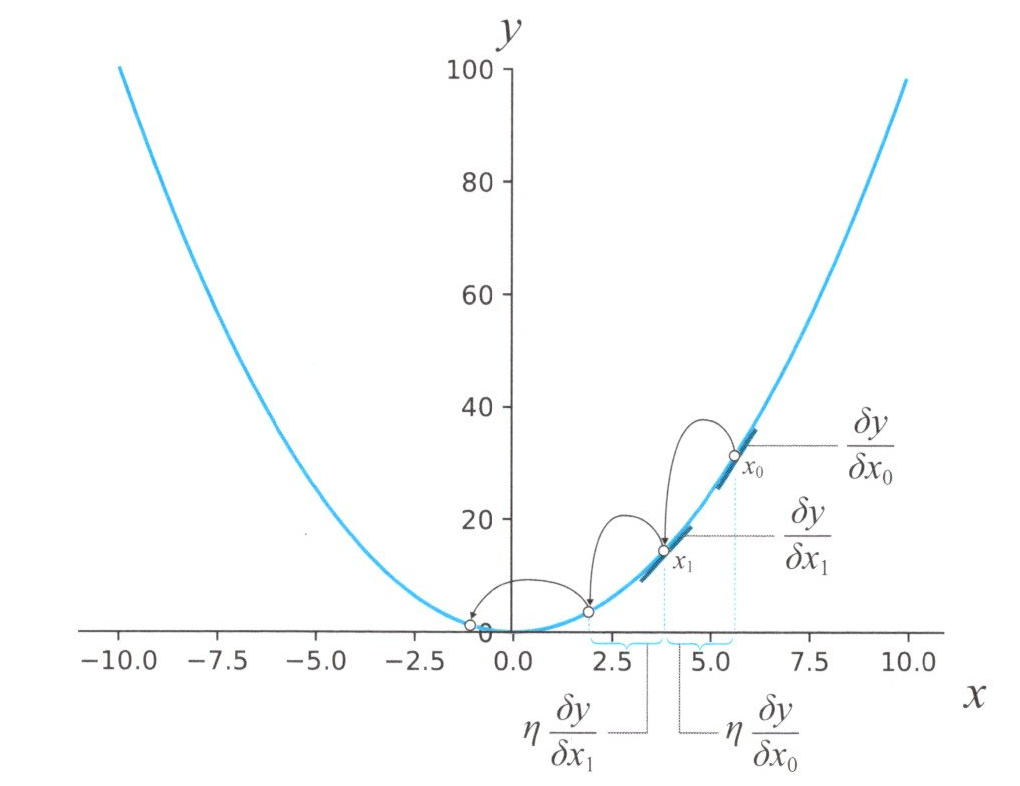
大股で最小値を探す
この様にニューラルネットワークのモデルに直接関係するパラメータ以外の\(η\)のようなパラメータをハイパーパラメータと呼びます。機械学習には、この他にもいろいろなハイパーパラメータがあるので、使いこなすにはある程度の知識が必須となります。
こういった具合で、ニューラルネットワークをはじめとする機械学習アルゴリズムは、正解データとの誤差が最小となるような出力が出来るように、あらゆるパラメータの組み合わせの中から、最適なものを見つけようとします。このような問題を最適化問題と呼び、様々な方法が提案されています、勾配法にもいろいろな方法があり、最急降下法、ニュートン法、確率的勾配法などが有名です。